题目内容
如图,在![]() 中,斜边
中,斜边![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 的外接圆
的外接圆![]() 与
与![]() 交于
交于![]() 点,过
点,过![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于
的延长线于![]() 点.
点.
1.求![]() 的半径;
的半径;
2.求线段![]() 的长.
的长.

1.证明:在Rt△ABC中,∠BAC=90°,∠C=30°,D为BC的中点,
∴∠ABD=60°,AD=BD=DC.
∴△ABD为等边三角形. AB=BD=6
∴O点为△ABD的中心(内心,外心,垂心三心合一).
连接OA,OB,过O作OM垂直于AB,∠BAO=∠OAD=30°
∴OA=2OM,AM=1/2AB=3
∴OA 2= OM2+AM2= ![]() +9
+9
∴OA=
2.![]()
解析:
1.由已知可得△ABD为等边三角形,连接OA,OB,过O作OM垂直于AB,利用勾股定理求得![]() 的半径
的半径
2.利用勾股定理求得AC的长,利用三角形ABC和三角形FDC相似,求得FC的长,可求得AF的长,在直角三角形AEF中, 利用勾股定理求得![]() 的长
的长

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
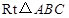 中,斜边
中,斜边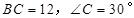 ,
,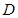 为
为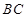 的中点,
的中点,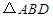 的外接圆
的外接圆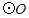 与
与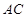 交于
交于 点,过
点,过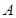 作
作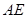 交
交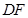 的延长线于
的延长线于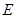 点.
点.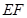 的长.
的长.
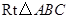 中,斜边
中,斜边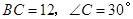 ,
,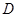 为
为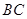 的中点,
的中点,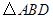 的外接圆
的外接圆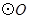 与
与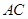 交于
交于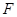 点,过
点,过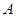 作
作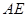 交
交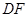 的延长线于
的延长线于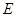 点.
点.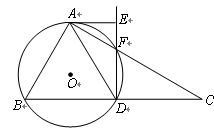
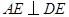 ;
;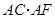 的值.
的值.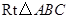 中,斜边
中,斜边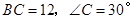 ,
,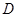 为
为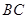 的中点,
的中点,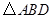 的外接圆
的外接圆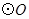 与
与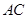 交于
交于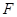 点,过
点,过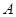 作
作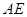 交
交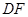 的延长线于
的延长线于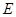 点.
点.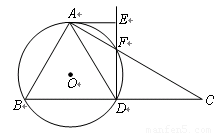
 ;
;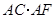 的值.
的值. 中,斜边
中,斜边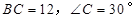 ,
,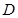 为
为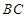 的中点,
的中点,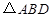 的外接圆
的外接圆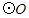 与
与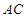 交于
交于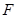 点,过
点,过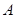 作
作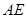 交
交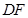 的延长线于
的延长线于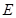 点.
点.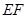 的长.
的长.