题目内容
如图,在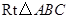 中,斜边
中,斜边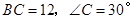 ,
,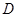 为
为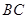 的中点,
的中点,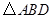 的外接圆
的外接圆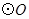 与
与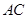 交于
交于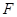 点,过
点,过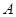 作
作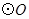 的切线
的切线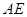 交
交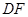 的延长线于
的延长线于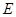 点.
点.
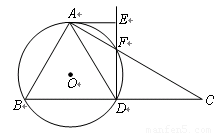
(1)求证: ;
;
(2)计算: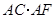 的值.
的值.
【答案】
(1)证明:在 中,
中, 为
为 的中点,
的中点,

 为等边三角形.
为等边三角形.
 点为
点为 的中心(内心,外心,垂心三心合一).
的中心(内心,外心,垂心三心合一).
∴连接OA,OB,


又 为
为 的切线,
的切线,

又四边形 内接于圆
内接于圆

 即
即
(2)解:由(1)知, 为等边三角形.
为等边三角形.

 则
则
 又
又
【解析】(1)连接OA、OB,证明△ABD为等边三角形后根据三心合一的定理求出∠OAC=60°,求出四边形ABDF内接于圆O,利用切线的性质求出AE⊥DE;
(2)由(1)可得△ABD为等边三角形,易证△ADF∽△ACD,可得AD2=AC•AF.

练习册系列答案
相关题目

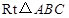 中,斜边
中,斜边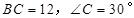 ,
,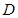 为
为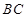 的中点,
的中点,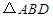 的外接圆
的外接圆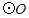 与
与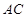 交于
交于 点,过
点,过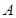 作
作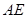 交
交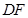 的延长线于
的延长线于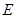 点.
点.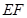 的长.
的长.
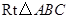 中,斜边
中,斜边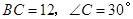 ,
,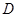 为
为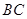 的中点,
的中点,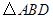 的外接圆
的外接圆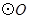 与
与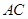 交于
交于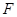 点,过
点,过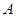 作
作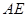 交
交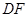 的延长线于
的延长线于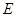 点.
点.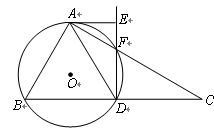
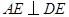 ;
;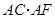 的值.
的值. 中,斜边
中,斜边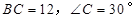 ,
,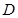 为
为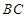 的中点,
的中点,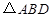 的外接圆
的外接圆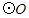 与
与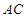 交于
交于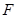 点,过
点,过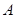 作
作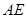 交
交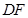 的延长线于
的延长线于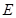 点.
点.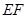 的长.
的长.