题目内容
观察下列方程及其解的特征:(1)x+
| 1 |
| x |
(2)x+
| 1 |
| x |
| 5 |
| 2 |
| 1 |
| 2 |
(3)x+
| 1 |
| x |
| 10 |
| 3 |
| 1 |
| 3 |
…
解答下列问题:
(1)请猜想:方程x+
| 1 |
| x |
| 26 |
| 5 |
(2)请猜想:关于x的方程x+
| 1 |
| x |
| 1 |
| a |
(3)下面以解方程x+
| 1 |
| x |
| 26 |
| 5 |
解:原方程可化为5x2-26x=-5.
(下面请大家用配方法写出解此方程的详细过程)
分析:解此题首先要认真审题,寻找规律,依据规律解题.解题的规律是将分式方程转化为一元二次方程,再采用配方法即可求得.而且方程的两根互为倒数,其中一根为分母,另一根为分母的倒数.
解答:解:(1)x1=5,x2=
;
(2)
(或a+
);
(3)方程二次项系数化为1,
得x2-
x=-1.
配方得,
x2-
x+(-
)2=-1+(-
)2,即(x-
)2=
,
开方得,
x-
=±
,
解得x1=5,x2=
.
经检验,x1=5,x2=
都是原方程的解.
| 1 |
| 5 |
(2)
| a2+1 |
| a |
| 1 |
| a |
(3)方程二次项系数化为1,
得x2-
| 26 |
| 5 |
配方得,
x2-
| 26 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
| 144 |
| 25 |
开方得,
x-
| 13 |
| 5 |
| 12 |
| 5 |
解得x1=5,x2=
| 1 |
| 5 |
经检验,x1=5,x2=
| 1 |
| 5 |
点评:此题考查了学生的综合应用能力,解题的关键是认真审题,寻找规律.
配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 的解为
的解为 ; (2)
; (2) 的解为
的解为 ;
; 的解为
的解为 ; …… ……
; …… …… 的解为 ;
的解为 ; 的方程
的方程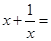 的解为
的解为 ;
; .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程) 的解为
的解为 ;
(2)
;
(2) 的解为
的解为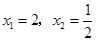 ;
; 的解为
的解为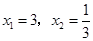 ; ……
……
; ……
…… 的解为 ;
的解为 ;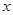 的方程
的方程 的解为
的解为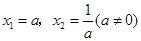 ;
; .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程)