题目内容
等腰三角形ABC的周长是30，且AB=2BC，则AB的长为
- A.15
- B.12
- C.10
- D.15或12
B
分析：由于AB、BC没有明确，哪边是底，哪边是腰，需分类讨论．
解答：解；设BC=x，则AB=2x；
当AB为底时，等腰三角形的三边长为x，x，2x；2x=x+x，不能构成三角形，此种情况不成立；
当AB为腰，BC为底时；x+2x+2x=30，解得x=6；
由于12-6＜6＜12+6，能构成三角形；此时AB=2x=12；
故选B．
点评：本题考查了等腰三角形的性质；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
分析：由于AB、BC没有明确，哪边是底，哪边是腰，需分类讨论．
解答：解；设BC=x，则AB=2x；
当AB为底时，等腰三角形的三边长为x，x，2x；2x=x+x，不能构成三角形，此种情况不成立；
当AB为腰，BC为底时；x+2x+2x=30，解得x=6；
由于12-6＜6＜12+6，能构成三角形；此时AB=2x=12；
故选B．
点评：本题考查了等腰三角形的性质；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
练习册系列答案
阅读快车系列答案
相关题目
如图1，Rt△ABC中，∠C=90°，AC=12，BC=5，点M在边AB上，且AM=6．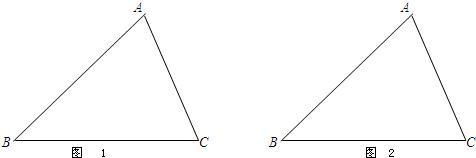
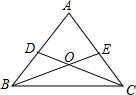在一次数学课上，周老师在屏幕上出示了一个例题：
，且
），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．
（1）小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”，从而平分蛋糕．