题目内容
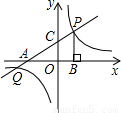
如图,直线 分别交x轴、y轴于点A、C,已知P是该直线在第一象限内的一点,PB⊥x轴于点B,S△APB=9.
分别交x轴、y轴于点A、C,已知P是该直线在第一象限内的一点,PB⊥x轴于点B,S△APB=9.(1)求△AOC的面积;
(2)求点P的坐标;
(3)设点R与点P在同一反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于点T,是否存在点R使得△BRT与△AOC相似,若存在,求点R的坐标;若不存在,说明理由.

【答案】分析:(1)分别令x=0以及y=0求出点A,C的坐标.从而求出△AOC的面积.
(2)证明△AOC∽△ABP,设PB=a,AB=2a,已知S△APB=9,求出a值后可求出点P的坐标.
(3)设△RBT∽△ACO,利用线段比求出R点坐标,RT,BT.当△RBT∽△CAO得出RT=n,BT=2n,R(2+2n,n)然后代入y= 求解.
求解.
解答:解:(1)A(-4,0),C(0,2),
△AOC的面积为4;(2分)
(2)∵△AOC∽△ABP,
∴设PB=a,AB=2a,
∵S△APB= a×2a=9,
a×2a=9,
解得a=±3(舍负)
即PB=3、AB=6 P的坐标为(2,3)(3分).
(3)由P(2,3)得反比例函数为 .(1分)
.(1分)
当△RBT∽△ACO时, ,
,
设BT=m,则RT=2m,R(2+m,2m),
代入 得,m1=-3(舍),m2=1,R(3,2).(3分)
得,m1=-3(舍),m2=1,R(3,2).(3分)
当△RBT∽△CAO时,
同理得:BT=2RT,设RT=n,BT=2n,得:R(2+2n,n),
代入 得:
得: (舍去负值),
(舍去负值),
R( +1,
+1, )(5分).
)(5分).
点评:本题考查的是一次函数的应用,相似三角形的判定等相关知识,综合性较强,难度中上.
(2)证明△AOC∽△ABP,设PB=a,AB=2a,已知S△APB=9,求出a值后可求出点P的坐标.
(3)设△RBT∽△ACO,利用线段比求出R点坐标,RT,BT.当△RBT∽△CAO得出RT=n,BT=2n,R(2+2n,n)然后代入y=
 求解.
求解.解答:解:(1)A(-4,0),C(0,2),
△AOC的面积为4;(2分)
(2)∵△AOC∽△ABP,
∴设PB=a,AB=2a,
∵S△APB=
 a×2a=9,
a×2a=9,解得a=±3(舍负)
即PB=3、AB=6 P的坐标为(2,3)(3分).
(3)由P(2,3)得反比例函数为
 .(1分)
.(1分)当△RBT∽△ACO时,
 ,
,设BT=m,则RT=2m,R(2+m,2m),
代入
 得,m1=-3(舍),m2=1,R(3,2).(3分)
得,m1=-3(舍),m2=1,R(3,2).(3分)当△RBT∽△CAO时,
同理得:BT=2RT,设RT=n,BT=2n,得:R(2+2n,n),
代入
 得:
得: (舍去负值),
(舍去负值),R(
 +1,
+1, )(5分).
)(5分).点评:本题考查的是一次函数的应用,相似三角形的判定等相关知识,综合性较强,难度中上.

练习册系列答案
相关题目
 曲线
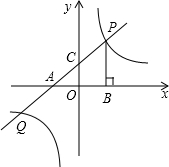
曲线 如图,直线l分别交x轴、y轴于A、B两点,且
如图,直线l分别交x轴、y轴于A、B两点,且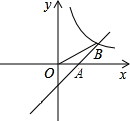 如图,直线y=x-1分别交x轴、反比例函数y=
如图,直线y=x-1分别交x轴、反比例函数y=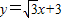 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
 x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y=
x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y= 在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.
在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.