Question

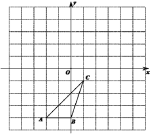
【题目】在平面直角坐标系中，已知点，将绕坐标原点顺时针旋转至，则点的坐标是(　　)

A.B.C.D.

Answer 1

【答案】B

【解析】

过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，根据旋转的性质可得OA=OA′，利用同角的余角相等求出∠OAB=∠A′OB′，然后利用“角角边”证明△AOB和△OA′B′全等，根据全等三角形对应边相等可得OB′=AB，A′B′=OB，然后写出点A′的坐标即可．

解：如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，

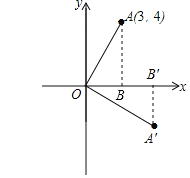
∵OA绕坐标原点O顺时针旋转90°至OA′，
∴OA=OA′，∠AOA′=90°，
∵∠A′OB′+∠AOB=90°，∠AOB+∠OAB=90°，
∴∠OAB=∠A′OB′，
在△AOB和△OA′B′中，

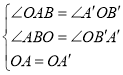
∴△AOB≌△OA′B′（AAS），
∴OB′=AB=4，A′B′=OB=3，
∴点A′的坐标为（4，-3）．
故选：B．