已知直线y=-x+2a和y=2x-a+3的交点在第二象限.则a的范围是 . 题目和参考答案——青夏教育精英家教网—

题目内容

已知直线y=-x+2a和y=2x-a+3的交点在第二象限，则a的范围是 .

-1＜a＜1．

解析试题分析：根据两直线相交的问题解方程组得交点坐标为（a-1，a+1），再根据第二象限点的坐标特征得到，然后解不等式组即可．
试题解析：解方程组得，
所以直线y=-x+2a和y=2x-a+3的交点坐标为（a-1，a+1），
根据题意得，
解得-1＜a＜1．
考点：两条直线相交或平行问题．

练习册系列答案

应用题卡系列答案

相关题目

计算：－2⁴－×[2－(－2)⁴]的结果为________．

如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12,动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒，y=S_△EPF，则y与t的函数图象大致是( )

如图，直线y=kx+b交坐标轴于A（﹣2，0），B（0，3）两点，则不等式kx+b＞0的解集是

一次函数的图像如图所示，则下列结论正确的是（）

A．，	B．，
C．，	D．，

直线y=2x－1沿y轴向上平移3个单位，则平移后直线与x轴的交点坐标为________．

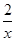如图，一次函数x=2与反比例函数y=和y=﹣的图象分别交于A、B两点，若P是y轴上任意一点，求△PAB的面积是_____________

如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm²，y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为．

如图，在平面直角坐标系中，已知点A（2，3），点B（﹣2，1），在x轴上存在点P到A，B两点的距离之和最小，则P点的坐标是．

试题分类