题目内容
 D为等边△ABC外一点,且BD=CD,∠BDC=120°,点M,N分别在AB,AC上,若BM+CN=MN,
D为等边△ABC外一点,且BD=CD,∠BDC=120°,点M,N分别在AB,AC上,若BM+CN=MN,求证:(1)∠MDN=60°;
(2)作出△DMN的高DH,并证明DH=BD.
分析:(1)延长NC到E,使CE=BM,连接DE,根据等腰三角形的性质以及等边三角形的性质可以得到△BDM和△CDE都是直角三角形,易证这两个三角形全等,根据全等三角形的性质即可证得;
(2)根据△MDN≌△EDN可以证得∠MND=∠DNE,然后根据角平分线的性质即可证得.
(2)根据△MDN≌△EDN可以证得∠MND=∠DNE,然后根据角平分线的性质即可证得.
解答: 证明:(1)延长NC到E,使CE=BM,连接DE.
证明:(1)延长NC到E,使CE=BM,连接DE.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=CD,∠BDC=120°,
∴∠CBD=∠BCD=30°,
∴∠ABD=∠ACD=90°,
在直角△BDM和直角△CDE中,
,
∴Rt△BDM≌Rt△CDE(SAS),
∴DM=DE,∠BDM=∠CDE,
∴∠MDE=∠BDC=120°,
∵BM+CN=MN,
∴MN=ME,
在△MDN和△EDN中,
,
∴△MDN≌△EDN(SSS),
∴∠MDN=∠EDN=60°;
(2)∵△MDN≌△EDN,
∴∠MND=∠DNE,
又∵DH⊥MN,DC⊥AC,
∴DH=DC,
∵BD=DC,
∴DH=BD.
 证明:(1)延长NC到E,使CE=BM,连接DE.
证明:(1)延长NC到E,使CE=BM,连接DE.∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=CD,∠BDC=120°,
∴∠CBD=∠BCD=30°,
∴∠ABD=∠ACD=90°,
在直角△BDM和直角△CDE中,
|
∴Rt△BDM≌Rt△CDE(SAS),
∴DM=DE,∠BDM=∠CDE,
∴∠MDE=∠BDC=120°,
∵BM+CN=MN,
∴MN=ME,
在△MDN和△EDN中,
|
∴△MDN≌△EDN(SSS),
∴∠MDN=∠EDN=60°;
(2)∵△MDN≌△EDN,
∴∠MND=∠DNE,
又∵DH⊥MN,DC⊥AC,
∴DH=DC,
∵BD=DC,
∴DH=BD.
点评:本题考查了全等三角形的判定与性质,以及角平分线的性质,正确作出辅助线,把BM+CN=MN转化成两条线段相等,构造全等的三角形是关键.

练习册系列答案
相关题目
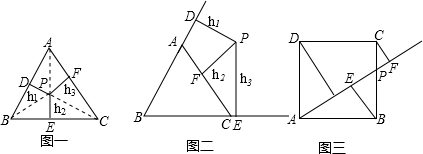
 22、有这样一个问题,如图,在等边△ABC外作一锐角∠PAC,在AP上截取AD=BC,为了求∠BDC的度数,小明做了如下提示:以A为圆心,以AB为半径作圆,
22、有这样一个问题,如图,在等边△ABC外作一锐角∠PAC,在AP上截取AD=BC,为了求∠BDC的度数,小明做了如下提示:以A为圆心,以AB为半径作圆,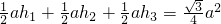 ,可得
,可得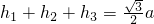 .
.

 ,可得
,可得 .
.