题目内容
如图,抛物线y=-x2+bx+c与直线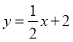 交于C、D两点,其中点C在y轴上,点D的坐标为(3,
交于C、D两点,其中点C在y轴上,点D的坐标为(3, ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F。
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F。
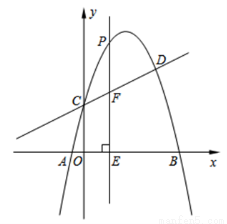
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个



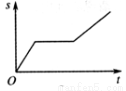
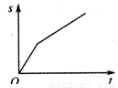
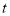 (h),航行的路程为
(h),航行的路程为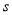 (km),则
(km),则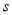 与
与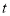 的函数图象大致是
的函数图象大致是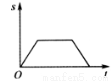
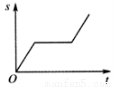
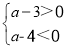
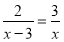

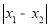 =4.
=4.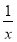 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+ 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论: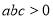 ;②
;② 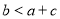 ; ③
; ③ 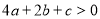 ;④
;④ 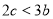 ;⑤
;⑤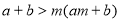 ,(
,(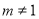 的实数)
的实数) 