题目内容
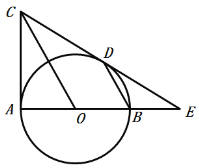
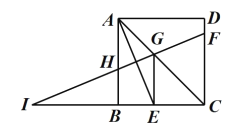
【题目】如图①,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的旋补三角形,△AB′C′边B′C′上的中线AD叫做△ABC的旋补中线.
如图②,当△ABC为等边三角形时,△AB′C′是△ABC的旋补三角形,AD是旋补中线,AD与BC的数量关系为:AD=_____BC;当BC=8时,则B′C′长为_____.
【答案】![]() 8
8![]()
【解析】
首先证明△ADB′是含有30°是直角三角形,可得AD=![]() AB′,然后解直角三角形即可得到结论.
AB′,然后解直角三角形即可得到结论.
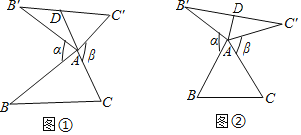
解:如图②中,
∵△ABC是等边三角形,
∴AB=BC=AC=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD=![]() AB′=
AB′=![]() BC,
BC,
∵BC=8,
∴AD=4,
∴B′D=![]() AD=4
AD=4![]() ,
,
∴B′C′=2B′D=8![]() ,
,
故答案为:![]() ,8
,8![]() .
.

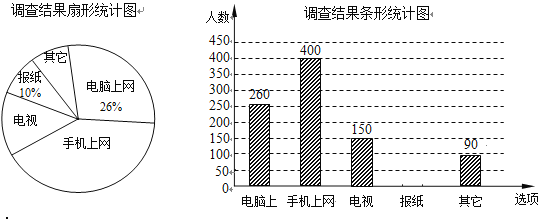
【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
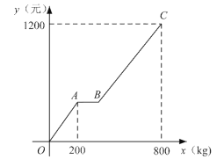
【题目】某商店代理销售一种水果,六月份的销售利润![]() (元)与销售量
(元)与销售量![]() 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今,一共售出 |
6月10、11日 | 这两天以成本价促销,之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图像中线段![]() 所在直线对应的函数表达式.
所在直线对应的函数表达式.