题目内容
若x2-y2=20,x-y=5,则x+y= ,x2+y2= ,xy= .
考点:平方差公式,完全平方公式
专题:计算题
分析:已知第一个等式左边利用平方差公式化简,把x-y=5代入求出x+y的值,与x-y联立求出x与y的值,即可确定出所求式子的值.
解答:解:∵x2-y2=(x+y)(x-y)=20,x-y=5,
∴x+y=4,
联立得:
,
解得:x=4.5,y=-0.5,
则x2+y2=20.25+0.25=21;xy=-2.25.
故答案为:4;21;-2.25
∴x+y=4,
联立得:
|
解得:x=4.5,y=-0.5,
则x2+y2=20.25+0.25=21;xy=-2.25.
故答案为:4;21;-2.25
点评:此题考查了平方差公式,完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
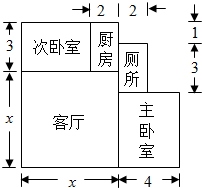 小李家住房结构如图所示,小李打算把主卧室、次卧室和客厅铺上强化木地板,把厕所和厨房铺上地砖.请解答下列问题:
小李家住房结构如图所示,小李打算把主卧室、次卧室和客厅铺上强化木地板,把厕所和厨房铺上地砖.请解答下列问题: