Question

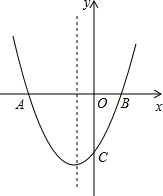（2012•路北区一模）如图，抛物线y=（x+1）²+k与x轴相交于A、B两点，与y轴相交于点C（0，-3）．
（1）求抛物线的对称轴及k值；
（2）抛物线的对称轴上存在一点P，使得PA+PC的值最小，求此时点P的坐标；
（3）点M是抛物线上一动点，且在第三象限，当M点运动到何处时，四边形AMCB的面积最大？求出四边形AMCB的最大面积及此时点M的坐标；
（4）若点E在抛物线的对称轴上，抛物线上是否存在点F，使以A、B、E、F为顶点的四边形为平行四边形？若存在，直接写出所有满足条件的点F的坐标；若不存在，请说明理由．

Answer 1

分析：（1）根据抛物线的顶点式即可得到抛物线的对称轴为直线x=-1，然后把C点坐标代入解析式可求出k=-4；
（2）令y=0得到（x+1）²-4=0，解得x₁=1，x₂=-3，可确定A点坐标为（-3，0），B点坐标为（1，0），再利用待定系数法确定直线AC的关系式为y=-x-3，由于使得PA+PC的值最小的点P为直线AC与对称轴的交点，把x=-1代入y=-x-3即可确定P点坐标；
（3）连接OM，设M点坐标为（x，（x+1）²-4），利用S_{四边形AMCB}=S_△AMO+S_△CMO+S_△CBO可得到S_{四边形AMCB}=-

3

2

x²-

9

2

x+6，配方得到S=-

3

2

（x+

3

2

）²+

75

8

，然后根据二次函数的最值问题得到当x=-

3

2

时，S最大，最大值为

75

8

；同时可得到M点坐标；
（4）讨论：当以AB为对角线，利用EA=EB和四边形AFBE为平行四边形得到四边形AFBE为菱形，则点F也在对称轴上，即F点为抛物线的顶点，所以F点坐标为（-1，-4）；当以AB为边时，根据平行四边形的性质得到EF=AB=4，则可确定F的横坐标，然后代入抛物线解析式得到F点的纵坐标．

解答：解：（1）抛物线的对称轴为直线x=-1，
把C（0，-3）代入y=（x+1）²+k得-3=1+k，
∴k=-4；
（2）连接AC，交对称轴于点P，如图1，
对于y=（x+1）²-4，令y=0，则（x+1）²-4=0，解得x₁=1，x₂=-3，
∴A点坐标为（-3，0），B点坐标为（1，0），
设直线AC的关系式为：y=mx+b，
把A（-3，0），C（0，-3）代入y=m x+b得

-3m+b=0 b=-3

，解得

m=-1 b=-3

，
∴直线AC的关系式为y=-x-3，
当x=-1时，y=1-3=-2，
∴P点坐标为（-1，-2）；
（3）连接OM，如图1，设M点坐标为（x，（x+1）²-4）
S_{四边形AMCB}=S_△AMO+S_△CMO+S_△CBO=

1

2

×AO×|y_m|+

1

2

×CO×|x_m|+

1

2

×OC×BO
=

3

2

[4-（x+1）²]+

1

2

×3×（-x）+

1

2

×3×1
=-

3

2

x²-

9

2

x+6
=-

3

2

（x+

3

2

）²+

75

8

，
当x=-

3

2

时，S最大，最大值为

75

8

；
此时M点坐标为（-

3

2

，-

15

4

）；
（4）存在．点F的坐标为（-1，-4）、（3，12）、（-5，12）．
当以AB为对角线，如图2，
∵四边形AFBE为平行四边形，
而EA=EB，
∴四边形AFBE为菱形，
∴点F也在对称轴上，即F点为抛物线的顶点，
∴F点坐标为（-1，-4）；
当以AB为边时，如图3，
∵四边形AFBE为平行四边形，
∴EF=AB=4，即F₂E=4，F₁E=4，
∴F₁的横坐标为3，F₂的横坐标为-5，
对于y=（x+1）²-4，
当x=3时，y=16-4=12；
当x=-5时，y=16-4=12，
∴F点坐标为（3，12）或（-5，12）．

点评：本题考查了二次函数综合题：二次函数y=ax²+bx+c（a、b、c为常数，a≠0）的图象为抛物线，其顶点式为y=a（x-

b

2a

）²+

4ac-b2

4a

，抛物线的对称轴为x=-

b

2a

，当a＞0，y_最小值=

4ac-b2

4a

；当a＜0，y_最，大值=

4ac-b2

4a

；抛物线上的点的横纵坐标满足抛物线的解析式；对于特殊四边形的判定与性质要熟练运用．