题目内容
【题目】如图，在O中，弦BC垂直于半径OA，垂足为E，D是优弧BC上一点，连接BD，AD，OC，∠ADB=30°.
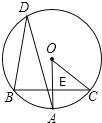
(1)求∠AOC的度数.
(2)若弦BC=8cm，求图中劣弧BC的长.
【答案】（1）60°；（2）
【解析】
（1）先根据垂径定理得出BE=CE，
，再根据圆周角定理即可得出∠AOC的度数；
（2）连接OB，先根据勾股定理得出OE的长，由弦BC=8cm，可得半径的长，继而求劣弧
的长；
解：
（1）连接OB，
∵BC⊥OA，
∴BE=CE，，
又∵∠ADB=30°，
∴∠AOC=∠AOB=2∠ADB，
∴∠AOC=60°；
（2）连接OB得，∠BOC=2∠AOC=120°，
∵弦BC=8cm，OA⊥BC，
∴CE=4cm，
∴OC=
cm，
∴劣弧的长为：
练习册系列答案
相关题目
