题目内容
 在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据
在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据 ≈1.73).
≈1.73).
解:在Rt△ACE中,∠ACE=30°,CE=BD=18,
∴tan∠ACE= ,
,
∴AE=CE•tan∠ACE=18•tan30°=6 ,
,
∴AB=AE+BE=6 +1.5≈10.4+1.5=11.9(米).
+1.5≈10.4+1.5=11.9(米).
分析:在Rt△ACE中,已知角的邻边求对边,可以用正切求AE,再加上BE即可.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
∴tan∠ACE=
 ,
,∴AE=CE•tan∠ACE=18•tan30°=6
 ,
,∴AB=AE+BE=6
 +1.5≈10.4+1.5=11.9(米).
+1.5≈10.4+1.5=11.9(米).分析:在Rt△ACE中,已知角的邻边求对边,可以用正切求AE,再加上BE即可.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
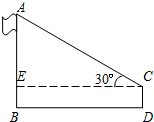 在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据
在学习了解直角三角形的有关知识后,一学习小组到操场测量学校旗杆的高度.如图,在测点D处安置测倾器,测得旗杆顶的仰角∠ACE的大小为30°,量得仪器的高CD为1.5米,测点D到旗杆的水平距离BD为18米,请你根据上述数据计算旗杆AB的高度(结果精确到0.1米;参考数据
 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73) 