题目内容
设x= ,y=
,y= ,则x5+x4y+xy4+y5的值为
,则x5+x4y+xy4+y5的值为
- A.47
- B.135
- C.141
- D.153
C
分析:先求出x+y、xy的值,把原式分解,再整体代入.
解答:∵x= ,y=
,y= ,
,
∴x+y=3,xy=1
∴x2+y2=(x+y)2-2xy=7,
∴x5+x4y+xy4+y5=(x5+x4y)+(xy4+y5)=x4(x+y)+y4(x+y)=(x4+y4)(x+y)=[(x2+y2)2-2x2y2](x+y)
=(49-2)×3=141.故选C.
点评:通过观察,必须运用因式分解达到降次的目的,同时通过提前计算有关x与y的和、积以及x2与y2的和与积,可降低难度.
分析:先求出x+y、xy的值,把原式分解,再整体代入.
解答:∵x=
 ,y=
,y= ,
,∴x+y=3,xy=1
∴x2+y2=(x+y)2-2xy=7,
∴x5+x4y+xy4+y5=(x5+x4y)+(xy4+y5)=x4(x+y)+y4(x+y)=(x4+y4)(x+y)=[(x2+y2)2-2x2y2](x+y)
=(49-2)×3=141.故选C.
点评:通过观察,必须运用因式分解达到降次的目的,同时通过提前计算有关x与y的和、积以及x2与y2的和与积,可降低难度.

练习册系列答案
相关题目
设x=
,y=
,则x5+x4y+xy4+y5的值为( )
3+
| ||
| 2 |
3-
| ||
| 2 |
| A、47 | B、135 |
| C、141 | D、153 |
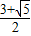 ,y=
,y=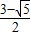 ,则x5+x4y+xy4+y5的值为( )
,则x5+x4y+xy4+y5的值为( ) ,y=
,y=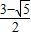 ,则x5+x4y+xy4+y5的值为( )
,则x5+x4y+xy4+y5的值为( )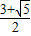 ,y=
,y=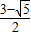 ,则x5+x4y+xy4+y5的值为( )
,则x5+x4y+xy4+y5的值为( )