题目内容
传统节日“春节”到来之际,某商店老板以每件60元的价格购进一批商品,若以单价80元销售,每月可售出300件.调查表明:单价每上涨1元,该商品每月的销售量就减少10件。
(1)请写出每月销售该商品的利润y(元)与单价x(元)间的函数关系式;
(2)单价定为多少元时,每月销售商品的利润最大?最大利润为多少?
(1)y=-10x2+100x+6000(0≤x≤30);(2) 单价定为5元时,每月销售商品的利润最大,最大利润为6250元.
【解析】
试题分析:(1)单价上涨x(元),由单价每上涨1元,该商品每月的销量就减少10件得到销售量为(300-10x)件,根据利润等于销售价减成本得到每件的利润为(80-60+x),因此每月销售该商品的利润y等于月销售量×每件的利润;
(2)把(1)得到的函数关系式进行配方得到y=-10(x-5)2+6250,然后根据二次函数的最值问题易得到单价定为多少元时,每月销售该商品的利润最大.
试题解析:(1)y=(80-60+x)(300-10x)
=-10x2+100x+6000(0≤x≤30);
(2)y=-10x2+100x+6000
=-10(x-5)2+6250
∵a=-10<0,
∴当x=5时,y有最大值,其最大值为6250,
即:单价定为5元时,每月销售商品的利润最大,最大利润为6250元.
考点:二次函数的应用.

练习册系列答案
相关题目
 的图像经过点(-2,4),且与正比例函数
的图像经过点(-2,4),且与正比例函数 的图像平行.
的图像平行. ),B(a+b,
),B(a+b, )为一次函数
)为一次函数 ,下列去分母正确的是( )
,下列去分母正确的是( ) B.
B.
 D.
D.

 B.
B.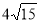 C.8 D.10
C.8 D.10 )图象如图所示,现有下列结论:①
)图象如图所示,现有下列结论:① 2-4
2-4
 >0 ②
>0 ②
 =0有两个相等的实数根,且满足
=0有两个相等的实数根,且满足 =
= ,试求
,试求 的值。
的值。 与
与 相似且面积比为4∶25,则
相似且面积比为4∶25,则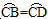 ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.
 有意义的x的取值范围是 .
有意义的x的取值范围是 .