题目内容
11.平面直角坐标系中的点P(2-m,$\frac{1}{2}$m)关于x轴的对称点在第四象限,则m的取值范围在数轴上可表示为0<m<2.分析 先根据x轴对称的点的坐标特点得到点P(2-m,$\frac{1}{2}$m)关于x轴对称的点的坐标为P1(2-m,-$\frac{1}{2}$m),然后根据第四象限点的坐标特点得到$\left\{\begin{array}{l}{2-m>0}\\{-\frac{1}{2}m<0}\end{array}\right.$,再解不等式组即可.
解答 解:点P(2-m,$\frac{1}{2}$m)关于x轴对称的点的坐标为P1(2-m,-$\frac{1}{2}$m),
∵P1(2-m,-$\frac{1}{2}$m)在第四象限,
∴$\left\{\begin{array}{l}{2-m>0}\\{-\frac{1}{2}m<0}\end{array}\right.$,
解得0<m<2,
∴m的取值范围为 0<m<2.
故答案为:0<m<2.
点评 本题考查了关于x轴、y轴对称的点的坐标:点P(a,b)关于x轴对称的点的坐标为P1(a,-b),关于y轴对称的点的坐标为P2(-a,b).也考查了解一元一次不等式组.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
6.由四舍五入法得到的近似数1.2×10-3,下列说法正确的是( )
| A. | 精确到百位,有2个有效数字 | B. | 精确到十分位,有2个有效数字 | ||
| C. | 精确到千分位,有2个有效数字 | D. | 精确到万分位,有2个有效数字 |
16.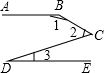 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )
 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=180° | C. | ∠1=∠2+∠3 | D. | ∠1-∠2+∠3=180° |
3.下列命题中,属于定义的是( )
| A. | 两点确定一条直线 | |
| B. | 两直线平行,内错角相等 | |
| C. | 点到直线的距离是该点到这条直线的垂线段的长度 | |
| D. | 同角或等角的余角相等 |
20.零是( )
| A. | 最小的正数 | B. | 最小的整数 | C. | 最大的负数 | D. | 绝对值最小的数 |
 用一些大小相同的正方体,摆成如图所示形状的立方体图形,画出从正面看,从左面看,从上面看这个立体图形得到的平面图形.
用一些大小相同的正方体,摆成如图所示形状的立方体图形,画出从正面看,从左面看,从上面看这个立体图形得到的平面图形. 如图,在四边形ABCD中,E是BC上一点,DE、AB的延长线交于点F,且AB=BF,DE=EF,S△SBE=S△DEF,求证:四边形ABCD为平行四边形.
如图,在四边形ABCD中,E是BC上一点,DE、AB的延长线交于点F,且AB=BF,DE=EF,S△SBE=S△DEF,求证:四边形ABCD为平行四边形. 如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.
如图,正方形ABCD的边长是2,M是AD的中点,E是AB边上的一动点.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG,FG.