题目内容
18.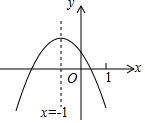 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1),其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1),其中结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线与x轴有两个交点得到b2-4ac>0,可判断①;根据对称轴是x=-1,可得x=-2、0时,y的值相等,所以4a-2b+c>0,可判断③;根据-$\frac{b}{2a}$=-1,得出b=2a,再根据a+b+c<0,可得$\frac{1}{2}$b+b+c<0,所以3b+2c<0,可判断②;x=-1时该二次函数取得最大值,据此可判断④.
解答 解:∵图象与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,
∴4ac-b2<0,
①正确;
∵-$\frac{b}{2a}$=-1,
∴b=2a,
∵a+b+c<0,
∴$\frac{1}{2}$b+b+c<0,3b+2c<0,
∴②是正确;
∵当x=-2时,y>0,
∴4a-2b+c>0,
∴4a+c>2b,
③错误;
∵由图象可知x=-1时该二次函数取得最大值,
∴a-b+c>am2+bm+c(m≠-1).
∴m(am+b)<a-b.故④正确
∴正确的有①②④三个,
故选C.
点评 本题考查二次函数图象与系数的关系,解题的关键是能看懂图象,利用数形结合的思想解答.

练习册系列答案
相关题目
8.下表是某校合唱团成员的年龄分布
对于不同的n,下列关于年龄的统计量不会发生改变的是( )
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | 10-n | n |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
3. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )| A. | 2 | B. | -1 | C. | $\sqrt{2}$ | D. | 4 |
7.某班级第3组第4排位置可以用数对(3,4)表示,则数对(1,2)表示的位置是( )
| A. | 第2组第1排 | B. | 第1组第1排 | C. | 第1组第2排 | D. | 第2组第2排 |
3.若反比例函数y=$\frac{k+1}{x}$的图象经过点(2,3),则k的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
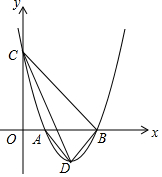 如图,抛物线y=a(x-1)(x-3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.
如图,抛物线y=a(x-1)(x-3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D. 如图,在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(x>0)的图象与直线y=x-2交于点A(3,m).
如图,在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(x>0)的图象与直线y=x-2交于点A(3,m).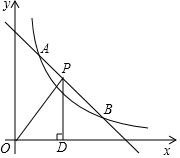 如图,一次函数y=-x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(m,3)和B(3,1).
如图,一次函数y=-x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(m,3)和B(3,1).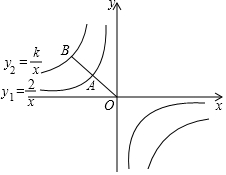 如图,已知点A,B分别在反比例函数y1=-$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,若点A是线段OB的中点,则k的值为-8.
如图,已知点A,B分别在反比例函数y1=-$\frac{2}{x}$和y2=$\frac{k}{x}$的图象上,若点A是线段OB的中点,则k的值为-8.