Question

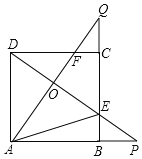
【题目】如图，矩形 中，点 ，点 分别在 轴， 轴上， 为边 上的一动点，现把 沿 对折， 点落在点 处．已知点 的坐标为 ．

(1) 当 点坐标为 时，求 点的坐标；

(2) 在点 沿 从点 运动至点 的过程中，设点 经过的路径长度为 ，求 的值；

(3) 在点 沿 从点 运动至点 的过程中，若点 落在同一条直线 上的次数为 次，请直接写出 的取值范围．

Answer 1

【答案】（1）点 的坐标为 ；（2）；(3) ．

【解析】试题分析:(1)依据题意画出图形,根据点D的坐标结合矩形的性质得出四边形OCDP是正方形,由此可得P点坐标,(2)由OP的长度为定值,可知点P的运动轨迹为以2为半径的圆弧,结合点B的坐标借助于特殊角的三角函数值得出∠COP=120°,再套用弧长公式即可得出结论,(3)取点E(0,4),过点E作圆O(弧CP段)的切线EP’,连接PP’,找出点P,P’的坐标,利用待定系数法求出k的值,再结合图形即可得出结论.

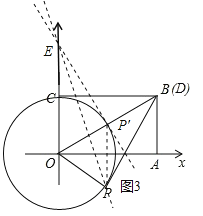
试题解析:(1)如图1,当D点坐标为（2,2）时,CD=2,因为OC=2,且四边形OABC为矩形,四边形OCDP是正方形,所以OP=2,所以点P的坐标为(2,0),

(2)如图2,因为在运动过程中,OP=OC始终成立,所以OP=2为定长,所以点P在以点O为圆心,以2为半径的圆上,因为点B的坐标为(,2),所以tan∠COB=,

所以∠COB=60°,∠COP=120°,所以弧长=,

(3)在图2的基础上,取点E(0,4),过点E作圆O(弧CP段)的切线EP’,切点为P’,连接PP’,因为OE=4,OP’=2,所以sin∠OEP’=,所以∠OEP’=30°,所以∠EOP’=60°,

因为∠COP=120°,所以∠POP’=60°,因为OP=OP’,所以三角形OPP’为等边三角形,

因为OP=2,所以P(),P’(),

当点P在直线y=kx+4上时,有-1=,所以k=,

当点P’在y=kx+4上时,有1=,所以k=,

综合可得:若点P落在同一条直线y=kx+4上的次数为2次,则k的取值范围为: .