题目内容
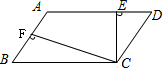 在?ABCD中,CE⊥AD于E,CF⊥AB于F.
在?ABCD中,CE⊥AD于E,CF⊥AB于F.
(1)证明:△BCF∽△DCE.
(2)若AD=4,DC=3,CE=2.5,求CF的长.
(1)证明:∵CE⊥AD,CF⊥AB
∴∠CED=∠CFB,
∵四边形为ABCD为平行四边形,
∴∠CBF=∠CDE,
∴△BCF∽△DCE;
(2)解:∵四边形为ABCD为平行四边形,AD=4,
∴BC=AD=4,
∵△BCF∽△DCE,
∴ =
= ,
,
∵DC=3,CE=2.5,
∴CF= .
.
答:CF的长为= .
.
分析:(1)根据CE⊥AD,CF⊥AB得出∠CED=∠CFB,再根据四边形为ABCD为平行四边形,得出∠CBF=∠CDE,然后利用相似三角形判定定理即可证明△BCF∽△DCE.
(2)根据四边形为ABCD为平行四边形,得出BC=AD=4,然后利用相似三角形性质,将已知数值代入即可求出CF的长.
点评:此题主要考查学生对相似三角形性质和平行四边形性质的理解和掌握,解答此题的关键是求证△BCF∽△DCE.
∴∠CED=∠CFB,
∵四边形为ABCD为平行四边形,
∴∠CBF=∠CDE,
∴△BCF∽△DCE;
(2)解:∵四边形为ABCD为平行四边形,AD=4,
∴BC=AD=4,
∵△BCF∽△DCE,
∴
 =
= ,
,∵DC=3,CE=2.5,
∴CF=
 .
.答:CF的长为=
 .
.分析:(1)根据CE⊥AD,CF⊥AB得出∠CED=∠CFB,再根据四边形为ABCD为平行四边形,得出∠CBF=∠CDE,然后利用相似三角形判定定理即可证明△BCF∽△DCE.
(2)根据四边形为ABCD为平行四边形,得出BC=AD=4,然后利用相似三角形性质,将已知数值代入即可求出CF的长.
点评:此题主要考查学生对相似三角形性质和平行四边形性质的理解和掌握,解答此题的关键是求证△BCF∽△DCE.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 12、如图,在?ABCD中,CE⊥AB,垂足为E,若∠A=120°,则∠BCE=
12、如图,在?ABCD中,CE⊥AB,垂足为E,若∠A=120°,则∠BCE= 在?ABCD中,CE⊥AD于E,CF⊥AB于F.
在?ABCD中,CE⊥AD于E,CF⊥AB于F.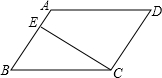 (2013•平南县二模)已知:如图:在?ABCD中,CE⊥AB,E为垂足,如果∠A=125°,则∠BCE的度数是( )
(2013•平南县二模)已知:如图:在?ABCD中,CE⊥AB,E为垂足,如果∠A=125°,则∠BCE的度数是( ) 如图,在?ABCD中,CE⊥AB,E为垂足,若AB=4,BC=6,则?ABCD的周长为
如图,在?ABCD中,CE⊥AB,E为垂足,若AB=4,BC=6,则?ABCD的周长为