题目内容
18.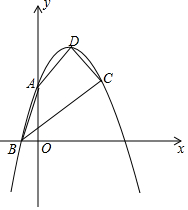 如图,抛物线y=ax2+bx+3(a≠0)与x轴的负半轴交于点B,与y轴交于点A,且OA=3OB,抛物线经过点(4,3),抛物线的顶点为点D.
如图,抛物线y=ax2+bx+3(a≠0)与x轴的负半轴交于点B,与y轴交于点A,且OA=3OB,抛物线经过点(4,3),抛物线的顶点为点D.(1)求这条抛物线的表达式;
(2)顺次连接A、B、C、D,求四边形ABCD的面积;
(3)如果点P在y轴上,且∠BPO=∠ABC,求点P的坐标.
分析 (1)求出确定点B坐标,把B(-1,0),C(4,3)代入y=ax2+bx+3得$\left\{\begin{array}{l}{a-b+3=0}\\{16a+4b+3=3}\end{array}\right.$,解方程组即可.
(2)首先证明AC∥x轴,根据S四边形ABCD=S△ACB+S△ACD计算即可.
(3)作AM⊥BC于M.根据S△ABC=$\frac{1}{2}$×3×4=$\frac{1}{2}$×$\sqrt{34}$•AM,推出AM=$\frac{6\sqrt{34}}{17}$,再求出BM,求出tan∠ABM=$\frac{AM}{BM}$=$\frac{6}{7}$,由∠BPO=∠ABC,可知tan∠BPO=$\frac{BO}{OP}$=$\frac{6}{7}$,求出OP即可解决问题.
解答 解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴的负半轴交于点B,与y轴交于点A,且OA=3OB,
∴A(0,3),OA=3,OB=1,
∴B(-1,0),
把B(-1,0),C(4,3)代入y=ax2+bx+3得$\left\{\begin{array}{l}{a-b+3=0}\\{16a+4b+3=3}\end{array}\right.$,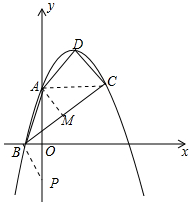
解得$\left\{\begin{array}{l}{a=-\frac{3}{5}}\\{b=\frac{12}{5}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{3}{5}$x+$\frac{12}{5}$x+3.
(2)∵y=-$\frac{3}{5}$x+$\frac{12}{5}$x+3=-$\frac{3}{5}$(x-2)2+$\frac{27}{5}$,
∴顶点D(2,$\frac{27}{5}$)
∵A(0,3),C(4,3),
∴AC∥x轴,
∴S四边形ABCD=S△ACB+S△ACD=$\frac{1}{2}$×4×3+$\frac{1}{2}$×4×($\frac{27}{5}$-3)=$\frac{54}{5}$.
(3)作AM⊥BC于M.
∵S△ABC=$\frac{1}{2}$×3×4=$\frac{1}{2}$×$\sqrt{34}$•AM,
∴AM=$\frac{6\sqrt{34}}{17}$,
在Rt△ABM中,AB=$\sqrt{10}$,AM=$\frac{6\sqrt{34}}{17}$,
∴BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\frac{7\sqrt{34}}{17}$,
∴tan∠ABM=$\frac{AM}{BM}$=$\frac{6}{7}$,
∵∠BPO=∠ABC,
∴tan∠BPO=$\frac{BO}{OP}$=$\frac{6}{7}$,
∴OP=$\frac{7}{6}$,
∴点P坐标(0,-$\frac{7}{6}$),根据对称性可知P′(0,$\frac{7}{6}$)也满足条件.
综上所述,满足条件的点P坐标为(0,$\frac{7}{6}$)或(0,-$\frac{7}{6}$).
点评 本题考查抛物线与x轴的交点、待定系数法、三角形面积、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形,属于中考常考题型.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 3.12×106 | B. | 3.12×105 | C. | 31.2×104 | D. | 0.312×7 |
| A. | 4 | B. | -2 | C. | 4或-2 | D. | 无法确定 |
| A. | x-3>y-3 | B. | x+3>y+2 | C. | -3x>-3y | D. | $\frac{x}{3}>\frac{y}{3}$ |
| A. | 4 | B. | ±4 | C. | ±2 | D. | 2 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无法确定 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | b÷2a2 | B. | 1$\frac{1}{2}$a2 | C. | -$\frac{3}{2}$a2×b | D. | $\frac{b}{2{a}^{2}}$ |
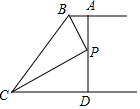 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )