题目内容
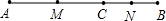如图，点C在线段AB上，点M、N分别是AC、BC的中点．若AC=9cm，CB=6cm，求线段MN的长．
解：∵M是AC的中点，
∴MC=
AC=×9=
，
∵N是BC的中点，
∴CN=BC=3，
∵MN=CN+CM，
∴MN=+3=
cm．
分析：首先根据点M、N分别是AC、BC的中点，求出MC和CN的长度，然后根据MN=CN+CM即可解答．
点评：本题主要考查比较线段的长短的知识点，结合图形解题直观形象，从图中很容易能看出各线段之间的关系．利用中点性质转化线段之间的倍分关系是解题的关键．
∴MC=
AC=×9=，∵N是BC的中点，
∴CN=
BC=3，∵MN=CN+CM，
∴MN=
+3=cm．分析：首先根据点M、N分别是AC、BC的中点，求出MC和CN的长度，然后根据MN=CN+CM即可解答．
点评：本题主要考查比较线段的长短的知识点，结合图形解题直观形象，从图中很容易能看出各线段之间的关系．利用中点性质转化线段之间的倍分关系是解题的关键．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
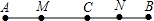
（1）已知：如图，点C在线段AB上，AC=18cm，BC=6cm，点M、N分别是AC、BC的中点，求MN的长；
如图，点M在线段AB上，MB=4cm，NB=9cm，且N是AM的中点，则AB=