Question

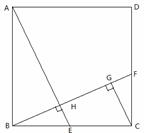
   如图，在正方形ABCD中，E是BC上的一点,连结AE，作BF⊥AE，垂足为H,交CD于F,作CG∥AE,交BF于G.

(1)求证CG=BH;

(2)FC²=BF·GF;

(3)=.

Answer 1

证明：（1）∵BF⊥AE，CG∥AE, CG⊥BF,

           ∴  CG⊥BF.

          ∵在正方形ABCD中，∠ABH+∠CBG=90^o, ∠CBG+∠BCG=90^o,

∠BAH+∠ABH=90^o,

∴∠BAH=∠CBG, ∠ABH=∠BCG, ……………………2分

AB=BC,

∴△ABH≌△BCG,

∴CG=BH;       ……………………4分

(2) ∵∠BFC=∠CFG, ∠BCF=∠CGF=90 ^o,

∴△CFG∽△BFC,

 ∴,

即FC²=BF·GF;                 ……………………7分

(3) 由（2）可知，BC²=BG·BF,

∵AB=BC,                

∴AB²=BG·BF,                     ……………………8分

∴==

即=                     ……………………9分