Question

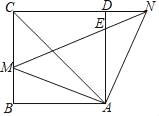
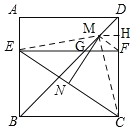
【题目】如图，四边形ABCD是边长为6的正方形，点E在边AB上，BE=4，过点E作EF∥BC，分别交BD，CD于G，F两点．若M，N分别是DG，CE的中点，则MN的长为（　 ）

A. 3 B. 4 C. D.

Answer 1

【答案】D

【解析】分析：作辅助线，构建全等三角形，证明△EMF≌△CMD，则EM=CM，利用勾股定理得：BD=，EC=，可得△EBG是等腰直角三角形，分别求EM=CM的长，利用勾股定理的逆定理可得△EMC是等腰直角三角形，根据直角三角形斜边中线的性质得MN的长．

详解：连接FM、EM、CM，

∵四边形ABCD为正方形，

∴∠ABC=∠BCD=∠ADC=90°，BC=CD，

∵EF∥BC，

∴∠GFD=∠BCD=90°，EF=BC，

∴EF=BC=DC，

∵∠BDC=∠ADC=45°，

∴△GFD是等腰直角三角形，

∵M是DG的中点，

∴FM=DM=MG，FM⊥DG，

∴∠GFM=∠CDM=45°，

∴△EMF≌△CMD，

∴EM=CM，

过M作MH⊥CD于H，

由勾股定理得：BD=，

EC=，

∵∠EBG=45°，

∴△EBG是等腰直角三角形，

∴EG=BE=4，

∴BG=4，

∴DM=，

∴MH=DH=1，

∴CH=61=5，

∴CM=EM=，

∵CE2=EM2+CM2，

∴∠EMC=90°，

∵N是EC的中点，

∴MN=EC=；

故选：D.