题目内容
12.写出一个根为$\sqrt{3}$和2的一元二次方程x2-(2+$\sqrt{3}$)x+2$\sqrt{3}$=0.分析 首先写出两根之和x1+x2=-(2+$\sqrt{3}$),再写出两根之积x1•x2=2$\sqrt{3}$,可直接得到方程.
解答 解:∵x1+x2=-(2+$\sqrt{3}$),x1•x2=2$\sqrt{3}$,
∴方程为:x2-(2+$\sqrt{3}$)x+2$\sqrt{3}$=0.
故答案为:x2-(2+$\sqrt{3}$)x+2$\sqrt{3}$=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列各组线段,能成比例的是( )
| A. | 3,6,9,18 | B. | 2,5,6,8 | C. | 1,2,3,4 | D. | 3,6,7,9 |
4.下列各式计算正确的是( )
| A. | 2$+\sqrt{2}$=2$\sqrt{2}$ | B. | 3$\sqrt{3}$-$\sqrt{2}$=2$\sqrt{2}$ | C. | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}$-$\sqrt{5}$ | D. | 2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$=3$\sqrt{2}$-2$\sqrt{3}$ |
2.下列说法正确的是( )
| A. | 能够完全重合的两个图形叫做全等图形 | |
| B. | 周长相等的三角形是全等三角形 | |
| C. | 各角相等的三角形是全等三角形 | |
| D. | 面积相等的三角形是全等三角形 |
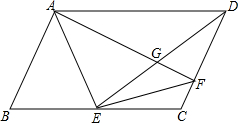 如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.
如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.