题目内容
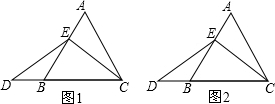
某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.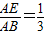 .点D在CB的延长线上,且ED=EC,求CD的长.
.点D在CB的延长线上,且ED=EC,求CD的长.(1)尝试探究
在图1中,过点E作EF∥BC,交AC于点F.先确定线段,AE与BD的大小关系是______,然后求出CD的长为______.
(2)类比延伸
如图2,在原题条件下,若
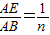 (n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.
(n>0),△ABC边长为m,则CD的长为______(用含n,m的代数式表示)试写出解答过程.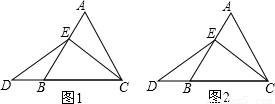
【答案】分析:(1)易证△AEF是等边三角形,则可以证明△BDE≌△FEC,即可证得EF=BD,则AE=BD可以证得;
(2)与(1)的证明完全相同,证明BD=AE,则求得BD的长,进而得到CD的长.
解答: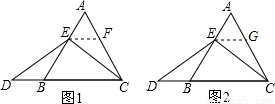 解:(1)∵EF∥BC,△ABC是等边三角形,
解:(1)∵EF∥BC,△ABC是等边三角形,
∴△AEF是等边三角形.
∴AE=EF=AF,
∴BE=CF.
∵ED=EC,
∴∠D=∠ECB,
∵EF∥BC,
∴∠ECB=∠FEC,
∴∠FEC=∠D,
∵∠AFE=∠ABC=60°,
∴∠EBD=∠CFE,
在△BDE和△FEC中,
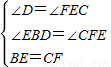 ,
,
∴△BDE≌△FEC(AAS),
∴EF=BD
又∵AE=EF,
∴AE=BD.
∴BD=AE= AB=
AB= ,
,
则CD=BC+BD=4+ =
=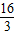 ;
;
(2)同(1)作EG∥BC,
则BD=AE=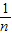 AB=
AB=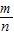 .
.
∴CD=BC+BD=m+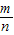 =
= .
.
故答案是:AE=BD,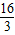 ;
;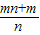 .
.
点评:本题考查了等边三角形的性质,以及全等三角形的判定与性质,证明BD=AE是关键.
(2)与(1)的证明完全相同,证明BD=AE,则求得BD的长,进而得到CD的长.
解答:
 解:(1)∵EF∥BC,△ABC是等边三角形,
解:(1)∵EF∥BC,△ABC是等边三角形,∴△AEF是等边三角形.
∴AE=EF=AF,
∴BE=CF.
∵ED=EC,
∴∠D=∠ECB,
∵EF∥BC,
∴∠ECB=∠FEC,
∴∠FEC=∠D,
∵∠AFE=∠ABC=60°,
∴∠EBD=∠CFE,
在△BDE和△FEC中,
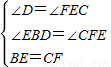 ,
,∴△BDE≌△FEC(AAS),
∴EF=BD
又∵AE=EF,
∴AE=BD.
∴BD=AE=
 AB=
AB= ,
,则CD=BC+BD=4+
 =
=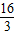 ;
;(2)同(1)作EG∥BC,
则BD=AE=
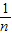 AB=
AB=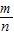 .
.∴CD=BC+BD=m+
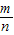 =
= .
.故答案是:AE=BD,
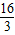 ;
;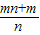 .
.点评:本题考查了等边三角形的性质,以及全等三角形的判定与性质,证明BD=AE是关键.

练习册系列答案
相关题目
 (2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.
(2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.