题目内容
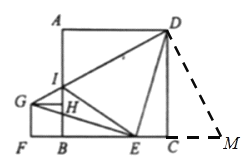
【题目】如图,点E是正方形ABCD的边BC上一点,连接DE,将DE绕着点E逆时针旋转90°,得到EG,过点G作GF⊥CB,垂足为F,GH⊥AB,垂足为H,连接DG,交AB于I.

(1)求证:四边形BFGH是正方形;
(2)求证:ED平分∠CEI;
(3)连接IE,若正方形ABCD的边长为3![]() ,则△BEI的周长为 .
,则△BEI的周长为 .
【答案】(1)见解析;(2)见解析;(3)6![]()
【解析】
(1)先证根据∠F=∠GHB=∠ABF=90°证得四边形BFGH为矩形,再证明△DCE≌△EFG进而可证得BF=FG,根据有一组邻边相等的矩形是正方形即可得证;
(2)延长EC到点M,使得CM=AI,连接DM,先证△ADI≌△CDM可得DI=DM,∠ADI=∠CDM,进而可证△EDM≌△EDI得∠DEI=∠DEC,即可得证;
(3)由(2)可知IE=EM=EC+CM=EC+AI,则△BEI的周长为BI+BE+IE=BI+BE+EC+AI=AB+BC,由此可求得答案.
(1)证明:∵将DE绕着点E逆时针旋转90°得到EG,
∴DE=EG,∠DEG=90°,
∴∠DEC+∠GEF=90°,
∵在正方形ABCD中
∴∠C=∠ABC=∠ABF=90°,BC=CD,
∴∠DEC+∠CDE=90°,
∴∠CDE=∠GEF,
∵GF⊥CB,GH⊥AB,
∴∠F=∠GHB=90°,
∴∠F=∠GHB=∠ABF=90°,
∴四边形BFGH为矩形,
在△DCE与△EFG中,
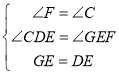
∴△DCE≌△EFG(AAS)
∴EF=CD,FG=CE,
∴EF=BC,
∴EF-BE=BC-BE,
即BF=CE,
∴BF=FG,
∴矩形BFGH为正方形;
(2)证明:如图,延长EC到点M,使得CM=AI,连接DM,
∵在正方形ABCD中
∴∠ADC=∠A=∠DCE=∠DCM=90°,AD=CD,
在△ADI与△CDM中,
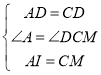
∴△ADI≌△CDM(SAS)
∴DI=DM,∠ADI=∠CDM,
∵DE=EG,∠DEG=90°,
∴∠EDG=∠EGD=45°,
又∵∠ADC=90°,
∴∠ADI+∠CDE=45°,
∴∠EDM=∠CDM+∠CDE=45°,
∴∠EDM=∠EDG,
在△EDM与△EDI中,
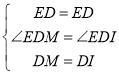
∴△EDM≌△EDI(SAS)
∴∠DEI=∠DEC,
∴DE平分∠IEC;
(3)解:由(2)可知△EDM≌△EDI,
∴IE=EM=EC+CM,
又∵CM=AI,
∴IE=EC+CM=EC+AI,
∴△BEI的周长为BI+BE+IE=BI+BE+EC+AI=AB+BC,
∵正方形ABCD的边长为3![]() ,
,
∴△BEI的周长为AB+BC=6![]() ,
,
故答案为:6![]() .
.