Question

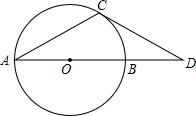
如图，在半径为1的⊙O中，AB为直径，C为弧AB的中点，D为弧CB的三等分点，且弧DB的长等于弧CD长的两倍，连接AD并延长交⊙O的切线CE于点E（C为切点），则AE的长为______．

Answer 1

连接OC，过A作AM⊥EC于M，
∵CE是圆O的切线，
∴OC⊥CE，
∵AM⊥EC，
∴AM∥OC，
∵C为弧AB的中点，
∴∠A=∠B=45°，AC=BC，
∵OA=OB，
∴CO⊥AB，
∴MA⊥AB，
∴四边形AMCO是矩形，
∴AM=OC=1，
∵D为弧CB的三等分点，
∴∠CAD=

1

3

×45°=15°，
∵MA⊥AB，OA为半径，
∴AM为圆O的切线，
∴∠MAC=∠B=45°，
∴∠MAD=15°+45°=60°，
∴∠AEM=180°-60°-90°=30°，
∴AE=2AM=2．
故答案为：2．