题目内容
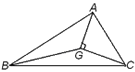
【题目】如图：在△ABC中，G是它的重心，AG⊥CD，如果
，则△AGC的面积的最大值是（ ）
A. 
B. 8 C. 
D. 6
【答案】B
【解析】延长BG交AC于D．由重心的性质得到 BG=2GD，D为AC的中点，再由直角三角形斜边上的中线等于斜边的一半，得到AC=2GD，即有BG=AC，从而得到AC、GD的长．当GD⊥AC时，△AGC的面积的最大，最大值为：
ACGD，即可得出结论．
延长BG交AC于D．
∵G是△ABC的重心，∴BG=2GD，D为AC的中点．
∵AG⊥CG，∴△AGC是直角三角形，∴AC=2GD，∴BG=AC．
∵BGAC=32，∴AC=
=
，GD=
．当GD⊥AC时，．△AGC的面积的最大，最大值为：ACGD=
=8．故选B．
练习册系列答案
相关题目
