题目内容
若关于x的方程 有实数根,则k的取值范围为
有实数根,则k的取值范围为
- A.k≥0
- B.k>0
- C.k≥
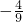
- D.k>
A
分析:若一元二次方程有两不等实数根,则根的判别式△=b2-4ac>0,建立关于k的不等式,求出k的取值范围.还要根据二次根式的意义可知k≥0,然后确定最后k的取值范围.
解答:∵关于x的方程 有实数根,
有实数根,
∴△=b2-4ac=(-3 )2+4=9k+4≥0,
)2+4=9k+4≥0,
解得:k≥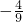 ,
,
又∵方程中含有
∴k≥0,
故本题选A.
点评:本题考查了一元二次方程根的判别式的应用.本题中需要注意的问题是k的值必须同时满足二次根式有意义和△≥0的条件,即要解不等式组,本题的易错点在于忽视了二次根式的条件而选取了C.
分析:若一元二次方程有两不等实数根,则根的判别式△=b2-4ac>0,建立关于k的不等式,求出k的取值范围.还要根据二次根式的意义可知k≥0,然后确定最后k的取值范围.
解答:∵关于x的方程
 有实数根,
有实数根,∴△=b2-4ac=(-3
 )2+4=9k+4≥0,
)2+4=9k+4≥0,解得:k≥
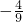 ,
,又∵方程中含有

∴k≥0,
故本题选A.
点评:本题考查了一元二次方程根的判别式的应用.本题中需要注意的问题是k的值必须同时满足二次根式有意义和△≥0的条件,即要解不等式组,本题的易错点在于忽视了二次根式的条件而选取了C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ=
如图,直线l与x轴交于点P(1,0),与x轴所夹的锐角为θ,且tanθ= ,直线l与抛物线
,直线l与抛物线 (a>0)相交于B(m,-3),D(3,n)
(a>0)相交于B(m,-3),D(3,n) 有实数根,求此时抛物线的解析式;
有实数根,求此时抛物线的解析式; 有实数根.
有实数根.  有实数根,则a的值可以是( )
有实数根,则a的值可以是( ) 有实数根.
有实数根.