Question

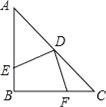
【题目】如图，在等边三角形ABC中，BD＝CE，将线段AE沿AC翻折，得到线段AM，连结EM交AC于点N，连结DM、CM．以下说法：①AD＝AM，②DE＝ME，③CN＝EC，④S△ABD＝S△ACM中，正确的是_____．

Answer 1

【答案】①③④

【解析】

证明△ABD≌△ACE（SAS），得出AD＝AE，∠BAD＝∠CAE，由折叠的性质得△ACM≌△ACE，得出△ABD≌△ACM，S△ABD＝S△ACM，故④正确；由全等三角形的性质和折叠的性质得出AD＝AE＝AM，故①正确，证出∠CEN＝30°，得出CN＝EC，故③正确；当∠DAE＝30°或DM⊥AE时，DE＝ME，故②错误；即可得出答案．

解：∵△ABC是等边三角形，

∴AB＝AC，∠B＝∠ACE＝∠BAC＝60°，

在△ABD和△ACE中， ，

∴△ABD≌△ACE（SAS），

∴AD＝AE，∠BAD＝∠CAE，

由折叠的性质得：△ACM≌△ACE，

∴△ABD≌△ACM，

∴S△ABD＝S△ACM，故④正确；

∵△ACM≌△ACE，

∴AE＝AM，CE＝CM，∠ACE＝∠ACM，

∴AD＝AE＝AM，故①正确，

∴AC垂直平分线段EM，

∵∠ECN＝60°，∠CNE＝90°，

∴∠CEN＝30°，

∴CN＝EC，故③正确；

当∠DAE＝30°或DM⊥AE时，DE＝ME，故②错误；

故答案为：①③④．