题目内容
（2013•河池）如图，在△ABC中，AC=6，BC=5，sinA=| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
分析：如图，过点C作CD⊥AB于点D．通过解直角△ACD可以求得CD=4；然后通过解直角△CDB来求tanB的值．
解答：
解：如图，过点C作CD⊥AB于点D．
∵在直角△ACD中，AC=6，sinA=
，
∴
=
=
，则CD=4．
∴在直角△CDB中，由勾股定理求得BD=
=
=3，
∴tanB=
=
．
故答案是：
．
解：如图，过点C作CD⊥AB于点D．∵在直角△ACD中，AC=6，sinA=
| 2 |
| 3 |
∴
| CD |
| AC |
| CD |
| 6 |
| 2 |
| 3 |
∴在直角△CDB中，由勾股定理求得BD=
| BC2-CD2 |
| 52-42 |
∴tanB=
| CD |
| BD |
| 4 |
| 3 |
故答案是：
| 4 |
| 3 |
点评：本题考查了解直角三角形．在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
互动课堂系列答案
相关题目
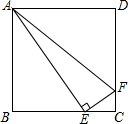（2013•河池）如图，正方形ABCD的边长为4，E、F分别是BC、CD上的两个动点，且AE⊥EF．则AF的最小值是
（2013•河池）如图，直线a∥b，直线c与a、b相交，∠1=70°，则∠2的大小是（ ）
（2013•河池）如图所示的几何体，其主视图是（ ）
（2013•河池）如图（1），已知两个全等三角形的直角顶点及一条直角边重合．将△ACB绕点C按顺时针方向旋转到△A′CB′的位置，其中A′C交直线AD于点E，A′B′分别交直线AD、AC于点F、G，则在图（2）中，全等三角形共有（ ）
（2013•河池）如图，AB为⊙O的直径，C为⊙O外一点，过点C作的⊙O切线，切点为B，连结AC交⊙O于D，∠C=38°．点E在AB右侧的半圆上运动（不与A、B重合），则∠AED的大小是（ ）