题目内容
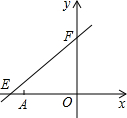 如图,直线y=
如图,直线y=| 3 |
| 4 |
| 3 |
| 4 |
(1)在点P运动过程中,试写出△OPA的面积s与x的函数关系式;
(2)当P运动到什么位置,△OPA的面积为
| 27 |
| 8 |
(3)过P作EF的垂线分别交x轴、y轴于C、D.是否存在这样的点P,使△COD≌△FOE?若存在,直接写出此时点P的坐标(不要求写解答过程);若不存在,请说明理由.
分析:(1)求出P的坐标,当P在第一、二象限时,根据三角形的面积公式求出面积即可;当P在第三象限时,根据三角形的面积公式求出解析式即可;
(2)把s的值代入解析式,求出即可;
(3)根据全等求出OC、OD的值,如图①所示,求出C、D的坐标,设直线CD的解析式是y=kx+b,把C(-6,0),D(0,-8)代入,求出直线CD的解析式,再求出直线CD和直线y=
x+6的交点坐标即可;如图②所示,求出C、D的坐标,求出直线CD的解析式,再求出直线CD和直线y=
x+6的交点坐标即可.
(2)把s的值代入解析式,求出即可;
(3)根据全等求出OC、OD的值,如图①所示,求出C、D的坐标,设直线CD的解析式是y=kx+b,把C(-6,0),D(0,-8)代入,求出直线CD的解析式,再求出直线CD和直线y=
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)∵P(x,y)代入y=
x+6得:y=
x+6,
∴P(x,
x+6),
当P在第一、二象限时,△OPA的面积是s=
OA×y=
×|-6|×(
x+6)=
x+18(x>-8)
当P在第三象限时,△OPA的面积是s=
OA×(-y)=-
x-18(x<-8)
答:在点P运动过程中,△OPA的面积s与x的函数关系式是s=
x+18(x>-8)或s=-
x-18(x<-8).
解:(2)把s=
代入得:
=
x+18或
=-
x-18,
解得:x=-6.5或x=-9.5,
x=-6.5时,y=
,
x=-9.5时,y=-1.125,
∴P点的坐标是(-6.5,
)或(-9.5,-1.125).
(3)解:假设存在P点,使△COD≌△FOE,
①如图所示:P的坐标是(-
,
);
②如图所示:
P的坐标是(
,
)
存在P点,使△COD≌△FOE,P的坐标是(-
,
)或(
,
).
| 3 |
| 4 |
| 3 |
| 4 |
∴P(x,
| 3 |
| 4 |
当P在第一、二象限时,△OPA的面积是s=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
当P在第三象限时,△OPA的面积是s=
| 1 |
| 2 |
| 9 |
| 4 |
答:在点P运动过程中,△OPA的面积s与x的函数关系式是s=
| 9 |
| 4 |
| 9 |
| 4 |
解:(2)把s=
| 27 |
| 8 |
| 27 |
| 8 |
| 9 |
| 4 |
| 27 |
| 8 |
| 9 |
| 4 |

解得:x=-6.5或x=-9.5,
x=-6.5时,y=
| 9 |
| 8 |
x=-9.5时,y=-1.125,
∴P点的坐标是(-6.5,
| 9 |
| 8 |
(3)解:假设存在P点,使△COD≌△FOE,

①如图所示:P的坐标是(-
| 168 |
| 25 |
| 24 |
| 25 |
②如图所示:

P的坐标是(
| 24 |
| 25 |
| 168 |
| 25 |
存在P点,使△COD≌△FOE,P的坐标是(-
| 168 |
| 25 |
| 24 |
| 25 |
| 24 |
| 25 |
| 168 |
| 25 |
点评:本题综合考查了三角形的面积,解二元一次方程组,全等三角形的性质和判定,用待定系数法求一次函数的解析式等知识点,此题综合性比较强,用的数学思想是分类讨论思想和数形结合思想,难度较大,对学生有较高的要求.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
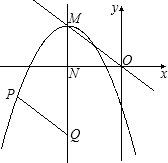 是抛物线对称轴上的动点.
是抛物线对称轴上的动点. 某条直线折叠,使点A落在y轴负半轴上的点D处,折痕与x轴交于点C.
某条直线折叠,使点A落在y轴负半轴上的点D处,折痕与x轴交于点C.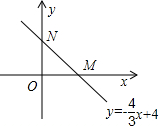 如图,直线
如图,直线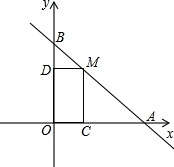 如图,直线
如图,直线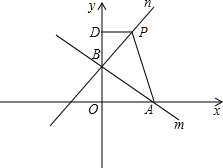 如图,直线
如图,直线