题目内容
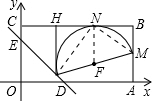
如图,在平面直角坐标中,矩形OABC,OA=4,AB=2,直线y=-x+
与坐标轴交于D,E两点,设M是AB的中点,P是线段DE上的动点.过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,梯形PMBH的面积是______.

| 3 |
| 2 |

设P(x,y),连接PN、MN、NF,
∵点P在y=-x+
上,
∴P(x,-x+
),
依题意知:PN⊥MN,FN⊥BC,F是圆心,
∴N是线段HB的中点,HN=NB=
,PH=2-(-x+
)=x+
,BM=1,
∵∠HPN+∠HNP=∠HNP+∠BNM=90°,
∴∠HPN=∠BNM,
又∵∠PHN=∠B=90°,
∴Rt△PNH∽Rt△NMB,
∴
=
,
∴
=
,
∴x2-12x+14=0,
解得:x=6+
(x>
舍去),x=6-
,
SPMBH=
=
=-
+
.
故答案为:-
+
.
∵点P在y=-x+
| 3 |
| 2 |
∴P(x,-x+
| 3 |
| 2 |
依题意知:PN⊥MN,FN⊥BC,F是圆心,
∴N是线段HB的中点,HN=NB=
| 4-x |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∵∠HPN+∠HNP=∠HNP+∠BNM=90°,
∴∠HPN=∠BNM,
又∵∠PHN=∠B=90°,
∴Rt△PNH∽Rt△NMB,
∴
| HN |
| BM |
| PH |
| BN |
∴
| ||
| 1 |
x+
| ||
|
∴x2-12x+14=0,
解得:x=6+
| 22 |
| 3 |
| 2 |
| 22 |
SPMBH=
| (BM+HP)•BH |
| 2 |
(1+6-
| ||||||
| 2 |
| 37 |
| 2 |
| 19 |
| 4 |
| 22 |
故答案为:-
| 37 |
| 2 |
| 19 |
| 4 |
| 22 |


练习册系列答案
相关题目

 与AB的延长线交于点D,CD=AO,如果AO>BO,且AO、BO是关于x的二次方程x2-14x+48=0的两个根.
与AB的延长线交于点D,CD=AO,如果AO>BO,且AO、BO是关于x的二次方程x2-14x+48=0的两个根.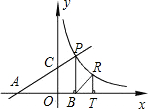 x轴于点B,S△APB=9.
x轴于点B,S△APB=9.

