题目内容
4．已知P=2a3-abc，Q=b2-c2+abc，M=a3+2b2-abc，且|b-8|+|c|+（a+7）2=0，求P-[2Q-3（M-P）]的值．分析 直接利用绝对值以及偶次方的性质得出a，b，c的值，再利用整式的加减运算法则化简求出答案．
解答 解：∵|b-8|+|c|+（a+7）2=0，
∴b=8，c=0，a=-7，
P-[2Q-3（M-P）]
=2a3-abc-{2（b2-c2+abc）-3[a3+2b2-abc-（2a3-abc）]}
=2a3-abc-[2b2-2c2+2abc-3a3-6b2+3abc+3（2a3-abc）]
=2a3-abc-（-4b2-2c2+2abc+3a3）
=-a3-3abc+4b2+2c2，
把b=8，c=0，a=-7代入上式得：
原式=343-0+256+0=599．
点评 此题主要考查了整式的加减运算以及偶次方和绝对值的性质，正确掌握整式加减运算法则是解题关键．
练习册系列答案
相关题目
10．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{3{a}^{2}}$ | B． | $\sqrt{\frac{1}{3}}$ | C． | $\sqrt{27}$ | D． | $\sqrt{35}$ |
11．若关于x的二次三项式x2-ax+36是一个完全平方式，那么a的值是（ ）
| A． | 12 | B． | ±12 | C． | 6 | D． | ±6 |
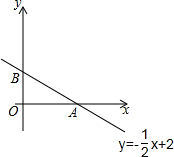在平面直角坐标系中，已知直线l：y=-$\frac{1}{2}$x+2交x轴于点A，交y轴于点B，直线l上的点P（m，n）在第一象限内，设△AOP的面积是S．