��Ŀ����
1��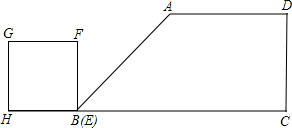 ��ֱ������ABCD�У�AD��BC����D=90�㣬AD=6��BC=14��DC=4���߳�Ϊ2��������EFGH����������ֱ��BC����1����λ/����ٶ��˶���H��E��B��C��ͬһֱ���ϣ���E��B�غϵ�E��C�غ�ʱֹͣ�˶������˶�ʱ��Ϊt�룬����AC��
��ֱ������ABCD�У�AD��BC����D=90�㣬AD=6��BC=14��DC=4���߳�Ϊ2��������EFGH����������ֱ��BC����1����λ/����ٶ��˶���H��E��B��C��ͬһֱ���ϣ���E��B�غϵ�E��C�غ�ʱֹͣ�˶������˶�ʱ��Ϊt�룬����AC����1������������ʱ��������EFGH�ĶԽ���EG����ֱ�߾�����A��
��2����ƽ�ƹ����У�������EFGH������ABCD�ص����ֵ����ΪS��ֱ��д��S��t֮��ĺ�����ϵʽ����д����Ӧ��t��ȡֵ��Χ��
��3����BC���е�ΪP��ֱ��HG��EF������B-A-C�ֱ���M��N���Ƿ����������tֵ��ʹ��P��M��NΪ�������������ֱ�������Σ������ڣ������Ӧ��tֵ���������ڣ���˵�����ɣ�
���� ��1��������AP��BC�ڵ�P���жϳ��ı���ADCP�Ǿ��Σ������Ƶ�CP=AD=6��AP=CD=4��Ȼ���жϳ���APEΪ����ֱ�������Σ����PE��BE�ij��ȸ��Ƕ��٣������жϳ�
����������ʱ��������EFGH�ĶԽ���EG����ֱ�߾�����A��
��2���������⣬��4��������ٵ�0��t��2ʱ���ڵ�2��t��4ʱ���۵�4��t��6ʱ���ܵ�6��t��14ʱ�����S��t֮��ĺ�����ϵʽ����д����Ӧ��t��ȡֵ��Χ���ɣ�
��3������t=5.6��ʹ��P��M��NΪ�������������ֱ�������Σ����ȸ��ݵ�P��BC���е㣬���BP��ֵ��Ȼ�����PN��MN��NE��BC���ɵ�BN2=BE•BP�������ֱ��������BNP�У����BN��ֵ���������BE��ֵ���жϳ���tΪ��ֵʱ����P��M��NΪ�������������ֱ�������μ��ɣ�
��� �⣺��1����ͼ1����AP��BC�ڵ�P��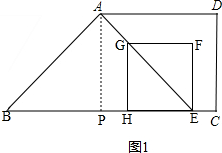 ��
��
��AP��BC����D=90�㣬AD��BC��
���ı���ADCP�Ǿ��Σ�
��CP=AD=6��AP=CD=4��
�֡�BC=14��
��BP=14-6=8��
��������EFGH�ĶԽ���EG����ֱ�߾�����Aʱ����AEP=45�㣬
�ߡ�APE=90�㣬
���EAP=90��-45��=45�㣬
���APEΪ����ֱ�������Σ�
��PE=AP=4��
��BE=BP+PE=8+4=12��
�ྭ��12��ʱ��������EFGH�ĶԽ���EG����ֱ�߾�����A��
��2���ٵ�0��t��2ʱ����ͼ2����AP��BC�ڵ�P����EF��AB���ڵ�I��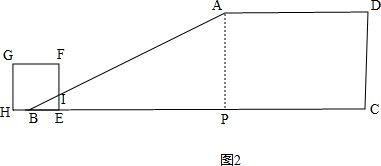 ��
��
�ɣ�1�����ɵ�
AP=4��BP=14-6=8��
��tan��ABP=$\frac{AP}{BP}=\frac{4}{8}=\frac{1}{2}$��
��IE=BE•tan��ABP=$\frac{1}{2}$t��
��S=$\frac{1}{2}BE•IE$=$\frac{1}{2}t•\frac{1}{2}t$=$\frac{1}{4}$t2��
�ڵ�2��t��4ʱ����ͼ3����EF��AB���ڵ�I��GH��AB���ڵ�K��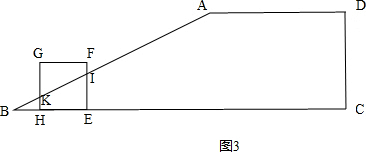 ��
��
��BE=t��
��IE=$\frac{1}{2}$BE=$\frac{1}{2}$t��
��BH=BE-HE=t-2��
��KH=$\frac{1}{2}$BH=$\frac{1}{2}$��t-2����
��S=S�ı���EIKH=$\frac{1}{2}$��IE+KH��•HE=$\frac{1}{2}��$[$\frac{1}{2}t$$+\frac{1}{2}$��t-2��]��2=t-1��
�۵�4��t��6ʱ����ͼ4����GF��AB���ڵ�O��GH��AB���ڵ�K��OQ��BC���Q��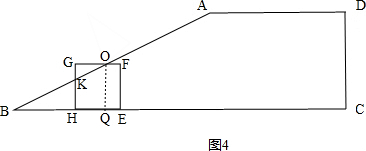 ��
��
��BH=BE-HE=t-2��
��KH=$\frac{1}{2}$BH=$\frac{1}{2}$��t-2����
��GK=2-KH=2-$\frac{1}{2}$��t-2��=3-$\frac{1}{2}t$��
��OQ=EF=2��
��BQ=2��$\frac{1}{2}$=4��
��HQ=BQ-BH=4-��t-2��=6-t��
��GO=HQ=6-t��
��S=2��2-$\frac{1}{2}$��3-$\frac{1}{2}$t����6-t��=-$\frac{1}{4}$t2+3t-5��
�ܵ�6��t��14ʱ����ͼ5��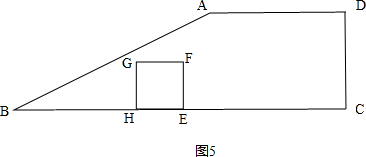 ��
��
S=S������EFGH=2��2=4��
���ϣ��ɵ�
S=$\left\{\begin{array}{l}{{\frac{1}{4}t}^{2}��0��t��2}\\{t-1��2��t��4}\\{-{\frac{1}{4}t}^{2}+3t-5��4��t��6}\\{4��6��t��14}\end{array}\right.$��
��3������t=5.6��ʹ��P��M��NΪ�������������ֱ�������Σ�
��ͼ6����PNM=90�㣬PN��MN��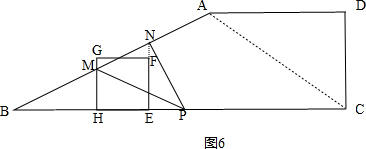 ��
��
�ߵ�P��BC���е㣬
��BP=$\frac{1}{2}BC$=$\frac{1}{2}��14$=7��
��PN��MN��NE��BC��
��BN2=BE•BP��
��tan��NBP=$\frac{1}{2}$��
��BN=2NP��
�ࣨ2NP��2+NP2=BP2=72=49��
���NP=$\frac{7}{5}\sqrt{5}$��
��BN=2NP=2��$\frac{7}{5}\sqrt{5}$=$\frac{14}{5}$$\sqrt{5}$��
�֡�BN2=BE•BP��
��BE=$\frac{{BN}^{2}}{BP}=\frac{{��\frac{14}{5}\sqrt{5}��}^{2}}{7}$=$\frac{\frac{196}{5}}{7}=5.6$��
�����t=5.6��ʹ��P��M��NΪ�������������ֱ�������Σ�
���� ��1��������Ҫ�������������ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã����������ν��˼���Ӧ�ã�Ҫ�������գ�
��2�����������ֱ�������ε����ʣ������Ρ����ε���������Լ������ε����ʺ�Ӧ�ã�Ҫ�������գ�

 ������������ϵ�д�
������������ϵ�д�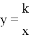 ͼ���ϵ������㣮��m��ֵ_____��
ͼ���ϵ������㣮��m��ֵ_____��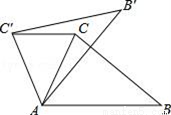
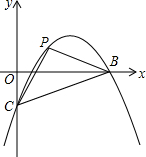 ��ͼ��������y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2��x�ύ��A��B����y�ύ�ڵ�C����PΪ��������һ�㣬�ҡ�PBC������Բ��Բ����x���ϣ����P�����꣮
��ͼ��������y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2��x�ύ��A��B����y�ύ�ڵ�C����PΪ��������һ�㣬�ҡ�PBC������Բ��Բ����x���ϣ����P�����꣮ ��ͼ����ABC����ADE��Ϊ�ȱ������Σ�����BD��CE�����߶�BD��CE��������ϵ��BD=CE��
��ͼ����ABC����ADE��Ϊ�ȱ������Σ�����BD��CE�����߶�BD��CE��������ϵ��BD=CE��