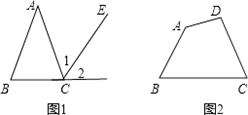
题目内容
阅读:如图1,CE∥AB,所以∠1=∠A,∠2=∠B.所以∠ACD=∠1+∠2=∠A+∠B.这是一个有用的结论,请用这个结论,在图2的四边形ABCD内引一条和一边平行的直线,则∠A+∠B+∠C+∠D=
360
360
度.
分析:可连接BD,作CE∥BD,则有∠ACF=∠1+∠2=∠CBD+∠BDC,再由题中的结论知,即可求出答案.
解答:解:由题意中的结论知,三角形的内角和等于一个平角的度数,为180度,连接BD,作CE∥BD,则有∠DCF=∠1+∠2=∠CBD+∠BDC,

∴∠BCD+∠1+∠2=∠CBD+∠BDC+∠BCD=180°,
∴∠A+∠ABC+∠BCD+∠ADC=180°×2=360°.

∴∠BCD+∠1+∠2=∠CBD+∠BDC+∠BCD=180°,
∴∠A+∠ABC+∠BCD+∠ADC=180°×2=360°.
点评:本题实际上是三角形内角和定理和四边形内角和定理的推导,利用平行线的性质和平角的概念即可求解.

练习册系列答案
相关题目