题目内容
（2008•顺义区二模）如图，AB是⊙O的直径，AC是弦，若AB=2，AC=| 3 |
分析：连接BC，依据圆周角定理即可证得△ABC是直角三角形．然后利用三角函数即可求得∠A的度数，根据等边对等角即可求得∠C的度数，再根据三角形的内角和定理即可求解．
解答：
解：连接BC．
∵AB是圆的直径，
∴∠ACB=90°，
∴在直角△ABC中，cosA=
=
，
∴∠A=30°，
∵OA=OC，
∴∠C=∠A=30°，
∴∠AOC=180°-∠A-∠C=180°-30°-30°=120°．
故选A．
解：连接BC．∵AB是圆的直径，
∴∠ACB=90°，
∴在直角△ABC中，cosA=
| AC |
| AB |
| ||
| 2 |
∴∠A=30°，
∵OA=OC，
∴∠C=∠A=30°，
∴∠AOC=180°-∠A-∠C=180°-30°-30°=120°．
故选A．
点评：本题考查了圆周角定理以及等腰三角形的性质，正确利用三角函数求得∠A的度数是关键．
练习册系列答案
相关题目
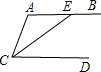（2008•顺义区二模）已知：如图，AB∥CD，CE平分∠ACD，交AB于点E，若∠A=110°，则∠BEC的度数是