题目内容
10.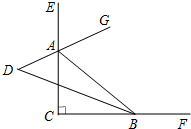 如图,∠ECF=90°,线段AB的端点分别在CE和CF上,BD平分∠CBA,并与∠CAB的外角平分线AG所在的直线交于一点D,
如图,∠ECF=90°,线段AB的端点分别在CE和CF上,BD平分∠CBA,并与∠CAB的外角平分线AG所在的直线交于一点D,(1)当∠CAB=50°,求∠D的度数.
(2)点A在射线CE上运动,(不与点C重合)时,∠D与∠C有怎样的数量关系?说说你的理由.
分析 (1)根据已知和邻补角的性质、互余的概念以及三角形的外角的性质求出∠D的度数;
(2)根据角平分线的定义和三角形的外角的性质计算即可.
解答 解:(1)∵∠CAB=50°,
∴∠EAB=130°,又AG是∠EAB的角平分线,
∴∠GAB=65°,
∵∠ECF=90°,∠CAB=50°,
∴∠ABC=40°,又BD平分∠CBA,
∴∠ABD=20°,
∴∠D=∠GAB-∠ABD=45°;
(2)∵AG是∠EAB的角平分线,
∴∠GAB=$\frac{1}{2}$∠EAB,
∵BD平分∠CBA,
∴∠ABD=$\frac{1}{2}$∠ABC,
∵∠EAB-∠ABC=90°,
∴∠D=∠GAB-∠ABD=45°,
∴∠D=$\frac{1}{2}$∠C.
点评 本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
20.下列几对数中,互为相反数的是( )
| A. | $\frac{3}{4}$和-0.75 | B. | -5和﹢3 | C. | $\frac{1}{3}$和0.3 | D. | $\frac{1}{2}$和-2 |
5.数轴上的点A到表示-1的点B距离是6,则点A表示的数为( )
| A. | 6或-6 | B. | 5 | C. | -7 | D. | 5或-7 |
2.在下列数-$\frac{5}{6}$,+1,6.7,-14,0,±3,-5,25%中,属于整数的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.已知在1个标准气压下,将1kg水的温度升高℃需要吸收4200J的热量,在同样的条件下,10kg水的温度升高50℃所吸收的热量用科学记数法表示为( )
| A. | 21×105J | B. | 2.1×105J | C. | 2.1×106J | D. | 0.21×107J |
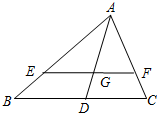 如图,在△ABC中,点G是△ABC的重心,过点G作EF∥BC,交AB于点E,交AC于点F,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{CA}=\overrightarrow b$,用向量$\overrightarrow a$和$\overrightarrow b$表示$\overrightarrow{EF}$.
如图,在△ABC中,点G是△ABC的重心,过点G作EF∥BC,交AB于点E,交AC于点F,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{CA}=\overrightarrow b$,用向量$\overrightarrow a$和$\overrightarrow b$表示$\overrightarrow{EF}$.