题目内容
14.计算:$\sqrt{\frac{3}{2}}$-$\sqrt{54}$÷2+(8-$\sqrt{3}$)(1+$\frac{1}{\sqrt{3}}$)分析 先进行二次根式的化简,然后合并.
解答 解:原式=$\frac{\sqrt{6}}{2}$-3$\sqrt{6}$÷2+8+$\frac{8\sqrt{3}}{3}$-1-$\sqrt{3}$
=-$\sqrt{6}$+$\frac{5\sqrt{3}}{3}$+7.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及合并.

练习册系列答案
相关题目
5. 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )
 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )| A. | AB⊥BC | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
9.某林业部门要查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
所以可以估计这种幼树移植成活的概率为( )
| 移植总数(n) | 成活数(m) | 成活的频率($\frac{m}{n}$) |
| 10 | 8 | 0.80 |
| 50 | 47 | 0.94 |
| 270 | 235 | 0.870 |
| 400 | 369 | 0.923 |
| 750 | 662 | 0.883 |
| 1500 | 1335 | 0.89 |
| 3500 | 3203 | 0.915 |
| 7000 | 6335 | 0.905 |
| 9000 | 8073 | 0.897 |
| 14000 | 12628 | 0.902 |
| A. | 0.1 | B. | 0.2 | C. | 0.8 | D. | 0.9 |
3.某学习小组为了了解某小区2000个成年人大约有多少人吸烟,随机抽查了200个成年人,结果其中有10个成年人吸烟,对于这个数据收集与处理的问题,下列说法正确的是( )
| A. | 该调查的方式是普查 | B. | 样本容量是200 | ||
| C. | 该小区只有190个成年人不吸烟 | D. | 该小区一定有100人吸烟 |
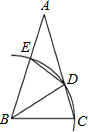 如图,在△ABC中,AB=AC,∠A=α.
如图,在△ABC中,AB=AC,∠A=α. 如图,双曲线y=$\frac{k}{x}$与y=-$\frac{3}{x}$分别为一第一、第四象限,A是y轴上任意一点,B是y=-$\frac{3}{x}$上的点,C是y=$\frac{k}{x}$上的点,线段BC⊥x轴于点D,且4BD=3CD,则下列说法:①双曲线y=$\frac{k}{x}$在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,-$\frac{4}{3}$);③△ABC的面积为定值7,正确的有( )
如图,双曲线y=$\frac{k}{x}$与y=-$\frac{3}{x}$分别为一第一、第四象限,A是y轴上任意一点,B是y=-$\frac{3}{x}$上的点,C是y=$\frac{k}{x}$上的点,线段BC⊥x轴于点D,且4BD=3CD,则下列说法:①双曲线y=$\frac{k}{x}$在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,-$\frac{4}{3}$);③△ABC的面积为定值7,正确的有( )