题目内容

有一张矩形纸片ABCD，AB= $数学公式$ ，AD= $数学公式$ ，将纸片折叠，使点D落在AB边上的D′处，折痕为AE，再将△AD′E以D′E为折痕向右折叠，使点A落在点A′处，设A′E与BC交于点F（如图），则A′F的长为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：利用折叠的性质，即可求得AD=AD′=A′D′= $\text{[math]}$ 、BD′=AB-AD= $\text{[math]}$ - $\text{[math]}$ ，A′E=AE= $\text{[math]}$ AD=2，又由相似三角形的对应边成比例，即可求得EF：A′F=EC：A′B，从而求得A′F的长度．
解答：

解：根据折叠的性质知，AD=AD′=A′D′= $\text{[math]}$ 、CE=CD-DE= $\text{[math]}$ - $\text{[math]}$ ，．
∵CE∥A′B，
∴△ECF∽△A′BF，
∴CE：BA′=EF：A′F（相似三角形的对应边成比例）；
又∵CE=CD-DE= $\text{[math]}$ - $\text{[math]}$ ，BA′=AD-CE=2 $\text{[math]}$ - $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ ；
而A′E=AE= $\text{[math]}$ AD=2，
∴A′F=4- $\text{[math]}$ ．
故选D．
点评：本题考查了翻折变换及正方形的性质，利用了折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等及正方形的性质，平行线的性质，有一定的难度．

练习册系列答案

相关题目

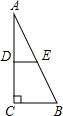如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有两个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（　　）

如图，在一张△ABC纸片中， ∠C＝90°， ∠B＝60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为

(　　)

A．1 B．2 C．3 D．4

如图1，已知有一张三角形纸片ABC的一边AB=10，若D为AB边上的点，过点D作DE//BC交AC于点E，分别过点D、E作DF⊥BC，EG⊥BC，垂足分别为点F、点G，把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠，点A、B、C分别落在A´、B´、C´处．若A´、B´、C´在矩形DFGE内或者其边上，且互不重合，此时我们称△A´B´C´（即图中阴影部分）为“重叠三角形”．

（1）实验操作：当AD=4时，①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，= ；
②若AB=AC，BC=12，如图3，= ；③若∠B=30°，∠C=45°，如图4，= ；
（2）实验探究：若△ABC为等边三角形（如图5），设AD的长为m，若重叠三角形A´B´C´存在，试用含m的代数式表示重叠三角形A´B´C´的面积，并写出m的取值范围．

（1）实验操作：当AD=4时，①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，= ；

②若AB=AC，BC=12，如图3，= ；③若∠B=30°，∠C=45°，如图4，= ；

（2）实验探究：若△ABC为等边三角形（如图5），设AD的长为m，若重叠三角形A´B´C´存在，试用含m的代数式表示重叠三角形A´B´C´的面积，并写出m的取值范围．

（2011•滨州）如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（　　）

A、1 B、2

C、3 D、4

有一张矩形纸片ABCD，AB=，AD=，将纸片折叠，使点D落在AB边上的D′处，折痕为AE，再将△AD′E以D′E为折痕向右折叠，使点A落在点A′处，设A′E与BC交于点F（如图），则A′F的长为

试题分类

有一张矩形纸片ABCD，AB= $数学公式$ ，AD= $数学公式$ ，将纸片折叠，使点D落在AB边上的D′处，折痕为AE，再将△AD′E以D′E为折痕向右折叠，使点A落在点A′处，设A′E与BC交于点F（如图），则A′F的长为