题目内容

一元二次方程x（x-7）=0根的情况是（　　）
A、有两个不相等的实数根
B、有两个相等的实数根
C、只有一个实数根
D、没有实数根
考点：根的判别式
专题：计算题
分析：先把方程化为一般式，再计算根的判别式，然后根据判别式的意义判断方程根的情况．
解答：解：x2-7x=0，
△=（-7）2-4×1×0=49＞0，
所以方程有两个不相等的实数根．
故选A．
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
3是
 
的平方根，
49
的算术平方根是
 
．
如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，若AD=5，DB=3，DE=4，则BC等于（　　）
A、
12
5
B、
15
4
C、
20
3
D、
32
5
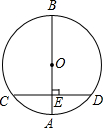如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段AE的长为（　　）
A、4B、3C、2D、6
下列运算正确的是（　　）
A、6
a
2
=
3a
B、-2
3
=
(-2)2×3
C、
16
1
3
=
16
×
1
3
D、
6
÷
2
=
3
在代数式中：-
x2
4
，3xy，
y
2x
，x2y-
x2
4
，
1
x
，
a
b
+x，
3x+4
5
，整式共有（　　）
A、3个B、4个C、5个D、6个
若代数式3x4y与-x2my是同类项，则常数m的值为（　　）
A、1B、2C、3D、4
已知：a=
1
3
+
2
，求
(a-
1
a
)2+4
 -
(a+
1
a
)2-4
 的值．
解方程：x2+3x=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网