Question

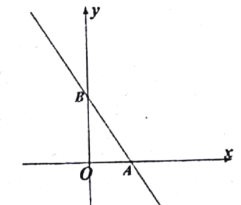
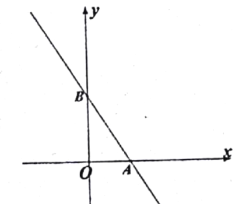
【题目】如图，在直角坐标系中，已知直线与轴相交于点，与轴交于点.

（1）求的值及的面积；

（2）点在轴上，若是以为腰的等腰三角形，直接写出点的坐标；

（3）点在轴上，若点是直线上的一个动点，当的面积与的面积相等时，求点的坐标.

Answer 1

【答案】（1）K=- ,的面积=3；（2）（2，0）或（2-）或C3（-2,0）；（3）（4，-3）或（-4,9）.

【解析】

①将代入直线可得K=- ，的面积=OB·OA＝＝3.

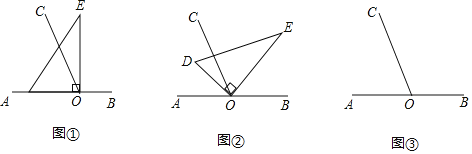
②如详解图，分类讨论c1,c2,求坐标.

③如详解图，分类讨论p1,p2,求坐标.

（1）将代入直线可得K=- ，点B坐标为（3,0），的面积=OB·OA·=2·3·=3.

②已知△ABC为等腰三角形，则AB=AC.可求出AB长为，以A为圆心，AB为半径画弧，与x轴交点有2个，易得C点坐标为C1（2，0）或C2（2-）.

以B为圆心，BA为半径画弧与x轴交点有一个，坐标为C3（-2,0）

③设P点坐标为（x,）

∵S△BAM=，∴P点在线段AB外.

若P在线段BA延长线上时，S△PBM=S△BAM+S△PAM

=

=

=3,x=4.

所以P坐标为（4，-3），

若P在线段AB延长线上，S△PBM=S△PAM－S△BAM=﹣

若﹣=3，x=-4,则P点为（-4,9）.