题目内容
10.已知二次函数y=x2-2ax+2a+3,当a=3或-1时,该函数y的最小值为0.分析 首先把y=0代入可得x2-2ax+2a+3=0,配方得(x-a)2-a2+2a+3=0,由(x-a)2≥0可得当-a2+2a+3=0时,y的最小值为0,再解即可.
解答 解:x2-2ax+2a+3=0,
(x-a)2-a2+2a+3=0,
当-a2+2a+3=0时,
a1=3或a2=-1,y的最小值为0.
故答案为:3或-1.
点评 此题主要考查了二次函数的最值,关键是正确掌握配方法的应用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.使代数式$\frac{1}{{x}^{2}-1}$+$\frac{1}{x+1}$+$\frac{1}{x-1}$等于0的x的值是( )
| A. | 3 | B. | 1 | C. | -1 | D. | -$\frac{1}{2}$ |
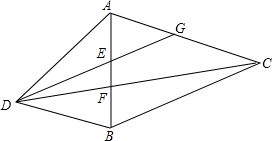 已知:CA=CB,AG=CG,AE=BE,∠ADB=∠CAB.求证:AF=DF.
已知:CA=CB,AG=CG,AE=BE,∠ADB=∠CAB.求证:AF=DF.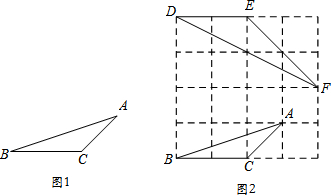
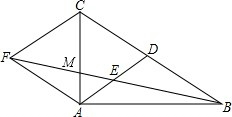 如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,BF交AC于点M,连接CF.
如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,BF交AC于点M,连接CF.