题目内容
已知一个半圆的圆心O在坐标原点,直径在x轴上,且与y轴交于点(0,1),该半圆的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线一定经过点
- A.(1,0)
- B.(-1,0)
- C.(0,-
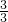 )
) - D.(0,-1)
D
分析:如图,设∠OPN的角平分线与y轴交于M点,PM是角平分线,所以∠1=∠2,PN垂直于x轴,所以,PN平行于y轴,所以∠1=∠3,所以∠2=∠3,所以OP=OM,即OM等于半径,所以M点坐标为(0,-1).
解答: 解:如图,
解:如图,
设∠OPN的角平分线与y轴交于M点,
∵PM是角平分线,∴∠1=∠2,
∵PN⊥x轴,∴PN∥y轴,
∴∠1=∠3,
∴∠2=∠3,
∴OP=OM,即OM等于半径,
∴M点坐标为(0,-1).
故选D.
点评:本题考查了垂径定理与坐标与图形的性质,以及角平分线的性质,是基础知识要熟练掌握.
分析:如图,设∠OPN的角平分线与y轴交于M点,PM是角平分线,所以∠1=∠2,PN垂直于x轴,所以,PN平行于y轴,所以∠1=∠3,所以∠2=∠3,所以OP=OM,即OM等于半径,所以M点坐标为(0,-1).
解答:
 解:如图,
解:如图,设∠OPN的角平分线与y轴交于M点,
∵PM是角平分线,∴∠1=∠2,
∵PN⊥x轴,∴PN∥y轴,
∴∠1=∠3,
∴∠2=∠3,
∴OP=OM,即OM等于半径,
∴M点坐标为(0,-1).
故选D.
点评:本题考查了垂径定理与坐标与图形的性质,以及角平分线的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
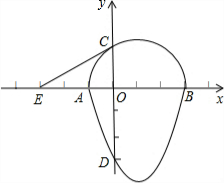 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是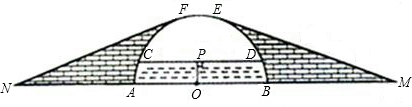

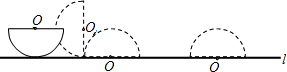 (2012•北塘区二模)已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移10米,半圆的直径为2米,则圆心O所经过的路线长是
(2012•北塘区二模)已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移10米,半圆的直径为2米,则圆心O所经过的路线长是