题目内容
（2011•翔安区质检）如图，为了增强同学们的数学应用意识，数学老师带某班数学课外活动小组去测量某段河流的宽度．同学们在点C处观测到对岸A点，测得∠ACB=45°，又在距C处60米远的D处测得∠ADB=30°，请你根据这些数据帮同学们算出河宽是多少？（精确到0.01m，已知
| 3 |
分析：如图所示，AB即为所求线段，而在三角形ACE中，由于∠ACB=45°故假设CE=AE=x，则BE=60+x，所以在三角形ABD中tan30°=
由此可以得到关于x的方程，然后解方程即可．
| AB |
| DB |
解答：解：如图，设河宽AB=x米，
由题意得：∠ABC=90°，
BC=AB=x米，BD=（x+60）米
在Rt△ABD中，
tan∠ADB=
=
=
∴3x=
x+60
x=30(1+
)=81.96（米）
答：河流的宽度约为81.96米
由题意得：∠ABC=90°，
BC=AB=x米，BD=（x+60）米
在Rt△ABD中，
tan∠ADB=
| AB |
| BD |
| x |
| x+60 |
| ||
| 3 |
∴3x=
| 3 |
| 3 |
x=30(1+
| 3 |
答：河流的宽度约为81.96米
点评：此题主要考查了三角函数的概念和应用，解题关键是把实际问题转化为数学问题，抽象到三角形中，利用三角函数进行解答．
练习册系列答案
相关题目
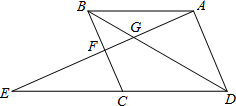（2011•翔安区质检）如图，点E为平行四边形ABCD中DC边的延长线上的点，且CE=DC，连接AE，分别交BC、BD于点F、G．
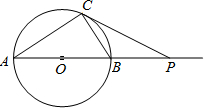（2011•翔安区质检）如图，⊙0的直径AB=6cm，P是AB延长线上的一点，过点P作⊙0的切线，切点为C，连接AC，BC．