Question

求证：以一个三角形三边中线为边的三角形的面积是原三角形面积的

3

4

．

Answer 1

分析：先写出已知求证，延长AD到G，使DG=AD，连接BG、GC，取BG中点H，连接FH、CH，则四边形ABGC为平行四边形，得AC=BG，
又因为E、H分别为AC、BG中点，得BH平行且等于EC，则HC=BE，同理得FH平行且等于AD，得到△FCH三边长即为△ABC三中线长，
然后依次求出S△BFH=

1

4

S△ABG=

1

4

×

1

2

S平行四边形ABGC=

1

4

S△ABC，S_△CAF=

1

2

S_△ABC，S_△CHG=

1

2

S_△CBG=

1

2

S_△ABC，最后得到S_△FCH=S_{平行四边形ABGC}-S_△BHF-S_△CHG-S_△CAF=2S_△ABC-

1

4

S_△ABC-

1

2

S_△ABC-

1

2

S_△ABC．

解答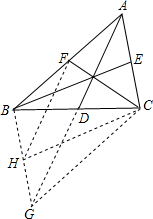：已知：AD，CF，BE是△ABC的三条中线．
求证：以AD，CF，BE为边的三角形的面积=

3

4

S_△ABC．
证明：如图，AD、BE、CF为△ABC的三条中线，延长AD到G，使DG=AD，连接BG、GC，
取BG中点H，连接FH、CH，
∴四边形ABGC为平行四边形，
∴AC=BG，
又因为E、H分别为AC、BG中点，
∴BH平行且等于EC，
∴四边形BHCE为平行四边形，
∴HC=BE，
又∵F、H为AB、BG中点，
∴FH平行且等于

1

2

AG，
∴FH平行且等于AD，
∴△FCH三边长即为△ABC三中线长，
又∵△BHF∽△ABG，

BF

AB

=

1

2

∴S△BFH=

1

4

S△ABG=

1

4

×

1

2

S平行四边形ABGC=

1

4

S△ABC，
∵S_△CAF=

1

2

S_△ABC，S_△CHG=

1

2

S_△CBG=

1

2

S_△ABC，
∴S_△FCH=S_{平行四边形ABGC}-S_△BHF-S_△CHG-S_△CAF=2S_△ABC-

1

4

S_△ABC-

1

2

S_△ABC-

1

2

S_△ABC=

3

4

S_△ABC．

点评：本题考查了相似三角形对应边的比相等．也考查了三角形中位线的性质以及平行四边形的性质．