题目内容
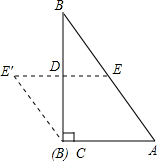 (2013•汕头)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是
(2013•汕头)如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,则四边形ACE′E的形状是平行四边形
平行四边形
.分析:四边形ACE′E的形状是平行四边形;首先根据三角形中位线的性质可得DE∥AC,DE=
AC,再根据旋转可得DE=DE′,然后可根据一组对边平行且相等的四边形是平行四边形进行判定即可.
| 1 |
| 2 |
解答:解:四边形ACE′E的形状是平行四边形;
∵DE是△ABC的中线,
∴DE∥AC,DE=
AC,
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,
∴DE=DE′,
∴EE′=2DE=AC,
∴四边形ACE′E的形状是平行四边形,
故答案为:平行四边形.
∵DE是△ABC的中线,
∴DE∥AC,DE=
| 1 |
| 2 |
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,
∴DE=DE′,
∴EE′=2DE=AC,
∴四边形ACE′E的形状是平行四边形,
故答案为:平行四边形.
点评:此题主要考查了图形的剪拼,以及平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
 (2013•汕头)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是
(2013•汕头)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (2013•汕头)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( )
(2013•汕头)如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,若∠2=50°,则∠1的大小是( ) (2013•汕头)如图,已知?ABCD.
(2013•汕头)如图,已知?ABCD. (2013•汕头)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(2013•汕头)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.