题目内容
 如图:已知AB∥ED,∠BCD=75°,则∠ABC+∠EDC=
如图:已知AB∥ED,∠BCD=75°,则∠ABC+∠EDC=考点:平行线的性质
专题:
分析:过点C作CF∥AB,根据平行公理可得CF∥DE,再根据两直线平行,内错角相等可得∠1=∠ABC,∠2=∠EDC,然后求出∠ABC+∠EDC=∠BCD.
解答: 解:如图,过点C作CF∥AB,
解:如图,过点C作CF∥AB,
则∠1=∠ABC,
∵AB∥ED,
∴CF∥DE,
∴∠2=∠EDC,
∴∠ABC+∠EDC=∠1+∠2=∠BCD,
∵∠BCD=75°,
∴∠ABC+∠EDC=75°.
故答案为:75°.
 解:如图,过点C作CF∥AB,
解:如图,过点C作CF∥AB,则∠1=∠ABC,
∵AB∥ED,
∴CF∥DE,
∴∠2=∠EDC,
∴∠ABC+∠EDC=∠1+∠2=∠BCD,
∵∠BCD=75°,
∴∠ABC+∠EDC=75°.
故答案为:75°.
点评:本题考查了平行线的性质,熟记性质是解题的关键,此类题目,难点在于过拐点作平行线.

练习册系列答案
相关题目
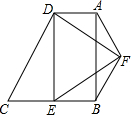 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=126°,则∠DBC的度数为
如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=126°,则∠DBC的度数为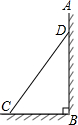 如图,铁管CD固定在墙角,BC=5米,∠BCD=55°,则顶端D的高度为
如图,铁管CD固定在墙角,BC=5米,∠BCD=55°,则顶端D的高度为