题目内容
已知x=
,则代数式4x4+4x3-9x2-2x+1的值为 .
| ||
| 2 |
考点:因式分解的应用
专题:计算题
分析:已知等式变形得到2x-1=
,两边平方,整理求出4x2-4x=1,原式变形后代入计算即可求出值.
| 2 |
解答:解:由x=
,得到2x-1=
,
两边平方:(2x-1)2=2,即4x2-4x+1=2,
∴4x2-4x=1,
则原式=4x4-4x3+8x3-9x2-2x+1=x2(4x2-4x)+8x3-9x2-2x+1
=x2+8x3-9x2-2x+1
=8x3-8x2-2x+1
=2x(4x2-4x)-2x+1
=2x-2x+1
=1.
故答案为:1.
| ||
| 2 |
| 2 |
两边平方:(2x-1)2=2,即4x2-4x+1=2,
∴4x2-4x=1,
则原式=4x4-4x3+8x3-9x2-2x+1=x2(4x2-4x)+8x3-9x2-2x+1
=x2+8x3-9x2-2x+1
=8x3-8x2-2x+1
=2x(4x2-4x)-2x+1
=2x-2x+1
=1.
故答案为:1.
点评:此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
 根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )
根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )| A、男生在13岁时身高增长速度最快 |
| B、女生在10岁以后身高增长速度放慢 |
| C、11岁时男女生身高增长速度基本相同 |
| D、9-10岁时女生身高比男生身高要高 |
为了考察某校七年级800名学生的视力情况,从中抽取50名学生进行视力检查,这个问题中的样本是( )
| A、800名学生的视力 |
| B、抽取的50名学生 |
| C、抽取的50名学生的视力 |
| D、每个学生的视力 |
已知x=1-a-b,y=1+ab,那么y=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
二次函数y=(x-2)2-3的图象上最低点的坐标是( )
| A、(-2,-3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(2,3) |
若三角形三个内角度数的比为2:3:4,则相应的外角比是( )
| A、2:3:4 |
| B、4:3:2 |
| C、7:6:5 |
| D、5:6:7 |
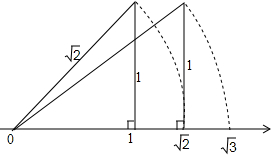 如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为
如图,由勾股定理:两条直角边长都为1的直角三角形,其斜边长为